Some Hints for Building Polygonal Models of Surfaces

Following are some techniques that you might want to use as you build polygonal approximations of surfaces. You might want to review this section after you've read Chapter 5 on lighting and Chapter 7 on display lists. The lighting conditions affect how models look once they're drawn, and some of the following techniques are much more efficient when used in conjunction with display lists. As you read these techniques, keep in mind that when lighting calculations are enabled, normal vectors must be specified to get proper results.

Constructing polygonal approximations to surfaces is an art, and there is no substitute for experience. This section, however, lists a few pointers that might make it a bit easier to get started.

  • Keep polygon orientations consistent. Make sure that when viewed from the outside, all the polygons on the surface are oriented in the same direction (all clockwise or all counterclockwise). Consistent orientation is important for polygon culling and two-sided lighting. Try to get this right the first time, since it's excruciatingly painful to fix the problem later. (If you use glScale*() to reflect geometry around some axis of symmetry, you might change the orientation with glFrontFace() to keep the orientations consistent.)
  • When you subdivide a surface, watch out for any nontriangular polygons. The three vertices of a triangle are guaranteed to lie on a plane; any polygon with four or more vertices might not. Nonplanar polygons can be viewed from some orientation such that the edges cross each other, and OpenGL might not render such polygons correctly.
  • There's always a trade-off between the display speed and the quality of the image. If you subdivide a surface into a small number of polygons, it renders quickly but might have a jagged appearance; if you subdivide it into millions of tiny polygons, it probably looks good but might take a long time to render. Ideally, you can provide a parameter to the subdivision routines that indicates how fine a subdivision you want, and if the object is farther from the eye, you can use a coarser subdivision. Also, when you subdivide, use large polygons where the surface is relatively flat, and small polygons in regions of high curvature.
  • For high-quality images, it's a good idea to subdivide more on the silhouette edges than in the interior. If the surface is to be rotated relative to the eye, this is tougher to do, since the silhouette edges keep moving. Silhouette edges occur where the normal vectors are perpendicular to the vector from the surface to the viewpoint - that is, when their vector dot product is zero. Your subdivision algorithm might choose to subdivide more if this dot product is near zero.
  • Try to avoid T-intersections in your models (see Figure 2-16). As shown, there's no guarantee that the line segments AB and BC lie on exactly the same pixels as the segment AC. Sometimes they do, and sometimes they don't, depending on the transformations and orientation. This can cause cracks to appear intermittently in the surface.

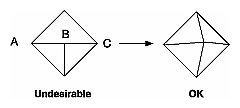
chap2-26.gif

Figure 2-16 : Modifying an Undesirable T-intersection

  • If you're constructing a closed surface, make sure to use exactly the same numbers for coordinates at the beginning and end of a closed loop, or you can get gaps and cracks due to numerical round-off. Here's a two-dimensional example of bad code:
·         /* don't use this code */
·         #define PI 3.14159265 
·         #define EDGES 30 
·          
·         /* draw a circle */
·         glBegin(GL_LINE_STRIP); 
·         for (i = 0; i <= EDGES; i++)
·             glVertex2f(cos((2*PI*i)/EDGES), sin((2*PI*i)/EDGES));
glEnd();

The edges meet exactly only if your machine manages to calculate the sine and cosine of 0 and of (2*PI*EDGES/EDGES) and gets exactly the same values. If you trust the floating-point unit on your machine to do this right, the authors have a bridge they'd like to sell you.... To correct the code, make sure that when i == EDGES, you use 0 for the sine and cosine, not 2*PI*EDGES/EDGES. (Or simpler still, use GL_LINE_LOOP instead of GL_LINE_STRIP, and change the loop termination condition to i < EDGES.)

An Example: Building an Icosahedron

To illustrate some of the considerations that arise in approximating a surface, let's look at some example code sequences. This code concerns the vertices of a regular icosahedron (which is a Platonic solid composed of twenty faces that span twelve vertices, each face of which is an equilateral triangle). An icosahedron can be considered a rough approximation for a sphere. Example 2-13 defines the vertices and triangles making up an icosahedron and then draws the icosahedron.

Example 2-13 : Drawing an Icosahedron

#define X .525731112119133606 
#define Z .850650808352039932
 
static GLfloat vdata[12][3] = {   
   {-X, 0.0, Z}, {X, 0.0, Z}, {-X, 0.0, -Z}, {X, 0.0, -Z},   
   {0.0, Z, X}, {0.0, Z, -X}, {0.0, -Z, X}, {0.0, -Z, -X},   
   {Z, X, 0.0}, {-Z, X, 0.0}, {Z, -X, 0.0}, {-Z, -X, 0.0}
};
static GLuint tindices[20][3] = { 
   {0,4,1}, {0,9,4}, {9,5,4}, {4,5,8}, {4,8,1},   
   {8,10,1}, {8,3,10}, {5,3,8}, {5,2,3}, {2,7,3},   
   {7,10,3}, {7,6,10}, {7,11,6}, {11,0,6}, {0,1,6},
   {6,1,10}, {9,0,11}, {9,11,2}, {9,2,5}, {7,2,11} };
int i;
 
glBegin(GL_TRIANGLES);   
for (i = 0; i < 20; i++) {   
   /* color information here */
   glVertex3fv(&vdata[tindices[i][0]][0]);
   glVertex3fv(&vdata[tindices[i][1]][0]);
   glVertex3fv(&vdata[tindices[i][2]][0]);
}
glEnd();

The strange numbers X and Z are chosen so that the distance from the origin to any of the vertices of the icosahedron is 1.0. The coordinates of the twelve vertices are given in the array vdata[][], where the zeroth vertex is {- &Xgr; , 0.0, &Zgr; }, the first is {X, 0.0, Z}, and so on. The array tindices[][] tells how to link the vertices to make triangles. For example, the first triangle is made from the zeroth, fourth, and first vertex. If you take the vertices for triangles in the order given, all the triangles have the same orientation.

The line that mentions color information should be replaced by a command that sets the color of the ith face. If no code appears here, all faces are drawn in the same color, and it'll be impossible to discern the three-dimensional quality of the object. An alternative to explicitly specifying colors is to define surface normals and use lighting, as described in the next subsection.

Note: In all the examples described in this section, unless the surface is to be drawn only once, you should probably save the calculated vertex and normal coordinates so that the calculations don't need to be repeated each time that the surface is drawn. This can be done using your own data structures or by constructing display lists. (See Chapter 7.)

Calculating Normal Vectors for a Surface

If a surface is to be lit, you need to supply the vector normal to the surface. Calculating the normalized cross product of two vectors on that surface provides normal vector. With the flat surfaces of an icosahedron, all three vertices defining a surface have the same normal vector. In this case, the normal needs to be specified only once for each set of three vertices. The code in Example 2-14 can replace the "color information here" line in Example 2-13 for drawing the icosahedron.

Example 2-14 : Generating Normal Vectors for a Surface

GLfloat d1[3], d2[3], norm[3];   
for (j = 0; j < 3; j++) {   
   d1[j] = vdata[tindices[i][0]][j] - vdata[tindices[i][1]][j];   
   d2[j] = vdata[tindices[i][1]][j] - vdata[tindices[i][2]][j];   
}
normcrossprod(d1, d2, norm); 
glNormal3fv(norm);

The function normcrossprod() produces the normalized cross product of two vectors, as shown in Example 2-15.

Example 2-15 : Calculating the Normalized Cross Product of Two Vectors

void normalize(float v[3]) {   
   GLfloat d = sqrt(v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);
   if (d == 0.0) {
      error("zero length vector");   
      return;
   }
   v[0] /= d; v[1] /= d; v[2] /= d;
}
 
void normcrossprod(float v1[3], float v2[3], float out[3]) 
{ 
   GLint i, j;
   GLfloat length;
 
   out[0] = v1[1]*v2[2] - v1[2]*v2[1];
   out[1] = v1[2]*v2[0] - v1[0]*v2[2];
   out[2] = v1[0]*v2[1] - v1[1]*v2[0];
   normalize(out);
}

If you're using an icosahedron as an approximation for a shaded sphere, you'll want to use normal vectors that are perpendicular to the true surface of the sphere, rather than being perpendicular to the faces. For a sphere, the normal vectors are simple; each points in the same direction as the vector from the origin to the corresponding vertex. Since the icosahedron vertex data is for an icosahedron of radius 1, the normal and vertex data is identical. Here is the code that would draw an icosahedral approximation of a smoothly shaded sphere (assuming that lighting is enabled, as described in Chapter 5):

glBegin(GL_TRIANGLES); 
for (i = 0; i < 20; i++) {   
      glNormal3fv(&vdata[tindices[i][0]][0]);
      glVertex3fv(&vdata[tindices[i][0]][0]);
      glNormal3fv(&vdata[tindices[i][1]][0]);
      glVertex3fv(&vdata[tindices[i][1]][0]);
      glNormal3fv(&vdata[tindices[i][2]][0]);
      glVertex3fv(&vdata[tindices[i][2]][0]);
}
glEnd();

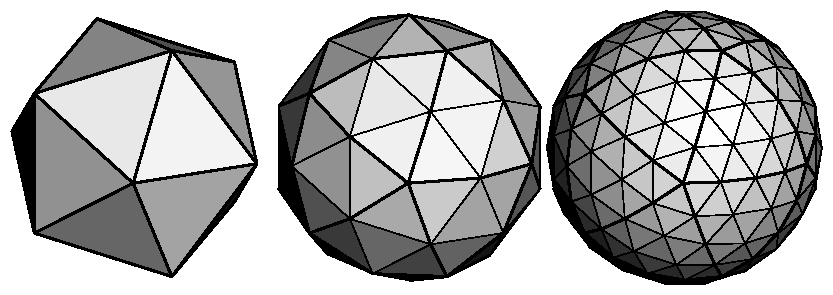
Improving the Model

A twenty-sided approximation to a sphere doesn't look good unless the image of the sphere on the screen is quite small, but there's an easy way to increase the accuracy of the approximation. Imagine the icosahedron inscribed in a sphere, and subdivide the triangles as shown in Figure 2-17. The newly introduced vertices lie slightly inside the sphere, so push them to the surface by normalizing them (dividing them by a factor to make them have length 1). This subdivision process can be repeated for arbitrary accuracy. The three objects shown in Figure 2-17 use 20, 80, and 320 approximating triangles, respectively.

icos.gif

Figure 2-17 : Subdividing to Improve a Polygonal Approximation to a Surface

Example 2-16 performs a single subdivision, creating an 80-sided spherical approximation.

Example 2-16 : Single Subdivision

void drawtriangle(float *v1, float *v2, float *v3) 
{ 
   glBegin(GL_TRIANGLES);
      glNormal3fv(v1); vlVertex3fv(v1);   
      glNormal3fv(v2); vlVertex3fv(v2);   
      glNormal3fv(v3); vlVertex3fv(v3);   
   glEnd();
}
 
void subdivide(float *v1, float *v2, float *v3) 
{ 
   GLfloat v12[3], v23[3], v31[3];   
   GLint i;
 
   for (i = 0; i < 3; i++) {
      v12[i] = v1[i]+v2[i];
      v23[i] = v2[i]+v3[i];    
      v31[i] = v3[i]+v1[i];   
   }
   normalize(v12);   
   normalize(v23);
   normalize(v31);
   drawtriangle(v1, v12, v31);   
   drawtriangle(v2, v23, v12);   
   drawtriangle(v3, v31, v23);   
   drawtriangle(v12, v23, v31);
}
 
for (i = 0; i < 20; i++) { 
   subdivide(&vdata[tindices[i][0]][0],      
             &vdata[tindices[i][1]][0],      
             &vdata[tindices[i][2]][0]);
}

Example 2-17 is a slight modification of Example 2-16 which recursively subdivides the triangles to the proper depth. If the depth value is 0, no subdivisions are performed, and the triangle is drawn as is. If the depth is 1, a single subdivision is performed, and so on.

Example 2-17 : Recursive Subdivision

void subdivide(float *v1, float *v2, float *v3, long depth)
{
   GLfloat v12[3], v23[3], v31[3];
   GLint i;
 
   if (depth == 0) {
      drawtriangle(v1, v2, v3);
      return;
   }
   for (i = 0; i < 3; i++) {
      v12[i] = v1[i]+v2[i];
      v23[i] = v2[i]+v3[i];
      v31[i] = v3[i]+v1[i];
   }
   normalize(v12);
   normalize(v23);
   normalize(v31);
   subdivide(v1, v12, v31, depth-1);
   subdivide(v2, v23, v12, depth-1);
   subdivide(v3, v31, v23, depth-1);
   subdivide(v12, v23, v31, depth-1);
}

Generalized Subdivision

A recursive subdivision technique such as the one described in Example 2-17 can be used for other types of surfaces. Typically, the recursion ends either if a certain depth is reached or if some condition on the curvature is satisfied (highly curved parts of surfaces look better with more subdivision).

To look at a more general solution to the problem of subdivision, consider an arbitrary surface parameterized by two variables u[0] and u[1]. Suppose that two routines are provided:

void surf(GLfloat u[2], GLfloat vertex[3], GLfloat normal[3]); 
float curv(GLfloat u[2]);

If surf() is passed u[], the corresponding three-dimensional vertex and normal vectors (of length 1) are returned. If u[] is passed to curv(), the curvature of the surface at that point is calculated and returned. (See an introductory textbook on differential geometry for more information about measuring surface curvature.)

Example 2-18 shows the recursive routine that subdivides a triangle either until the maximum depth is reached or until the maximum curvature at the three vertices is less than some cutoff.

Example 2-18 : Generalized Subdivision

void subdivide(float u1[2], float u2[2], float u3[2],
                float cutoff, long depth)
{
   GLfloat v1[3], v2[3], v3[3], n1[3], n2[3], n3[3];
   GLfloat u12[2], u23[2], u32[2];
   GLint i;
 
   if (depth == maxdepth || (curv(u1) < cutoff &&
       curv(u2) < cutoff && curv(u3) < cutoff)) {
      surf(u1, v1, n1); surf(u2, v2, n2); surf(u3, v3, n3);
      glBegin(GL_POLYGON);
         glNormal3fv(n1); glVertex3fv(v1);
         glNormal3fv(n2); glVertex3fv(v2);
         glNormal3fv(n3); glVertex3fv(v3);
      glEnd();
      return;
   }
   for (i = 0; i < 2; i++) {
      u12[i] = (u1[i] + u2[i])/2.0;
      u23[i] = (u2[i] + u3[i])/2.0;
      u31[i] = (u3[i] + u1[i])/2.0;
   }
   subdivide(u1, u12, u31, cutoff, depth+1);
   subdivide(u2, u23, u12, cutoff, depth+1);
   subdivide(u3, u31, u23, cutoff, depth+1);
   subdivide(u12, u23, u31, cutoff, depth+1);
}