Describing Points, Lines, and Polygons

This section explains how to describe OpenGL geometric primitives. All geometric primitives are eventually described in terms of their vertices - coordinates that define the points themselves, the endpoints of line segments, or the corners of polygons. The next section discusses how these primitives are displayed and what control you have over their display.

What Are Points, Lines, and Polygons?

You probably have a fairly good idea of what a mathematician means by the terms point, line, and polygon. The OpenGL meanings are similar, but not quite the same.

One difference comes from the limitations of computer-based calculations. In any OpenGL implementation, floating-point calculations are of finite precision, and they have round-off errors. Consequently, the coordinates of OpenGL points, lines, and polygons suffer from the same problems.

Another more important difference arises from the limitations of a raster graphics display. On such a display, the smallest displayable unit is a pixel, and although pixels might be less than 1/100 of an inch wide, they are still much larger than the mathematician's concepts of infinitely small (for points) or infinitely thin (for lines). When OpenGL performs calculations, it assumes points are represented as vectors of floating-point numbers. However, a point is typically (but not always) drawn as a single pixel, and many different points with slightly different coordinates could be drawn by OpenGL on the same pixel.

Points

A point is represented by a set of floating-point numbers called a vertex. All internal calculations are done as if vertices are three-dimensional. Vertices specified by the user as two-dimensional (that is, with only x and y coordinates) are assigned a z coordinate equal to zero by OpenGL.

Advanced

OpenGL works in the homogeneous coordinates of three-dimensional projective geometry, so for internal calculations, all vertices are represented with four floating-point coordinates (x, y, z, w). If w is different from zero, these coordinates correspond to the Euclidean three-dimensional point (x/w, y/w, z/w). You can specify the w coordinate in OpenGL commands, but that's rarely done. If the w coordinate isn't specified, it's understood to be 1.0. (See Appendix F for more information about homogeneous coordinate systems.)

Lines

In OpenGL, the term line refers to a line segment, not the mathematician's version that extends to infinity in both directions. There are easy ways to specify a connected series of line segments, or even a closed, connected series of segments (see Figure 2-2). In all cases, though, the lines constituting the connected series are specified in terms of the vertices at their endpoints.

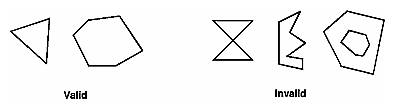
Figure 2-2 : Two Connected Series of Line Segments

Polygons

Polygons are the areas enclosed by single closed loops of line segments, where the line segments are specified by the vertices at their endpoints. Polygons are typically drawn with the pixels in the interior filled in, but you can also draw them as outlines or a set of points. (See "Polygon Details.")

In general, polygons can be complicated, so OpenGL makes some strong restrictions on what constitutes a primitive polygon. First, the edges of OpenGL polygons can't intersect (a mathematician would call a polygon satisfying this condition a simple polygon). Second, OpenGL polygons must be convex, meaning that they cannot have indentations. Stated precisely, a region is convex if, given any two points in the interior, the line segment joining them is also in the interior. See Figure 2-3 for some examples of valid and invalid polygons. OpenGL, however, doesn't restrict the number of line segments making up the boundary of a convex polygon. Note that polygons with holes can't be described. They are nonconvex, and they can't be drawn with a boundary made up of a single closed loop. Be aware that if you present OpenGL with a nonconvex filled polygon, it might not draw it as you expect. For instance, on most systems no more than the convex hull of the polygon would be filled. On some systems, less than the convex hull might be filled.

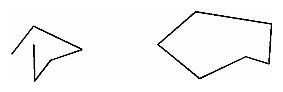
Figure 2-3 : Valid and Invalid Polygons

The reason for the OpenGL restrictions on valid polygon types is that it's simpler to provide fast polygon-rendering hardware for that restricted class of polygons. Simple polygons can be rendered quickly. The difficult cases are hard to detect quickly. So for maximum performance, OpenGL crosses its fingers and assumes the polygons are simple.

Many real-world surfaces consist of nonsimple polygons, nonconvex polygons, or polygons with holes. Since all such polygons can be formed from unions of simple convex polygons, some routines to build more complex objects are provided in the GLU library. These routines take complex descriptions and tessellate them, or break them down into groups of the simpler OpenGL polygons that can then be rendered. (See "Polygon Tessellation" in Chapter 11 for more information about the tessellation routines.)

Since OpenGL vertices are always three-dimensional, the points forming the boundary of a particular polygon don't necessarily lie on the same plane in space. (Of course, they do in many cases - if all the z coordinates are zero, for example, or if the polygon is a triangle.) If a polygon's vertices don't lie in the same plane, then after various rotations in space, changes in the viewpoint, and projection onto the display screen, the points might no longer form a simple convex polygon. For example, imagine a four-point quadrilateral where the points are slightly out of plane, and look at it almost edge-on. You can get a nonsimple polygon that resembles a bow tie, as shown in Figure 2-4, which isn't guaranteed to be rendered correctly. This situation isn't all that unusual if you approximate curved surfaces by quadrilaterals made of points lying on the true surface. You can always avoid the problem by using triangles, since any three points always lie on a plane.

Figure 2-4 : Nonplanar Polygon Transformed to Nonsimple Polygon

Rectangles

Since rectangles are so common in graphics applications, OpenGL provides a filled-rectangle drawing primitive, glRect*(). You can draw a rectangle as a polygon, as described in "OpenGL Geometric Drawing Primitives," but your particular implementation of OpenGL might have optimized glRect*() for rectangles.

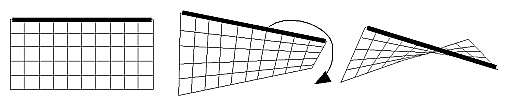
void glRect{sifd}(TYPEx1, TYPEy1, TYPEx2, TYPEy2);
void glRect{sifd}v(TYPE*v1, TYPE*v2);

Draws the rectangle defined by the corner points (x1, y1) and (x2, y2). The rectangle lies in the plane z=0 and has sides parallel to the x- and y-axes. If the vector form of the function is used, the corners are given by two pointers to arrays, each of which contains an (x, y) pair.

Note that although the rectangle begins with a particular orientation in three-dimensional space (in the x-y plane and parallel to the axes), you can change this by applying rotations or other transformations. (See Chapter 3 for information about how to do this.)

Curves and Curved Surfaces

Any smoothly curved line or surface can be approximated - to any arbitrary degree of accuracy - by short line segments or small polygonal regions. Thus, subdividing curved lines and surfaces sufficiently and then approximating them with straight line segments or flat polygons makes them appear curved (see Figure 2-5). If you're skeptical that this really works, imagine subdividing until each line segment or polygon is so tiny that it's smaller than a pixel on the screen.

Figure 2-5 : Approximating Curves

Even though curves aren't geometric primitives, OpenGL does provide some direct support for subdividing and drawing them. (See Chapter 12 for information about how to draw curves and curved surfaces.)

Specifying Vertices

With OpenGL, all geometric objects are ultimately described as an ordered set of vertices. You use the glVertex*() command to specify a vertex.

void glVertex{234}{sifd}[v](TYPEcoords);

Specifies a vertex for use in describing a geometric object. You can supply up to four coordinates (x, y, z, w) for a particular vertex or as few as two (x, y) by selecting the appropriate version of the command. If you use a version that doesn't explicitly specify z or w, z is understood to be 0 and w is understood to be 1. Calls to glVertex*() are only effective between a glBegin() and glEnd() pair.

Example 2-2 provides some examples of using glVertex*().

Example 2-2 : Legal Uses of glVertex*()

glVertex2s(2, 3); 

glVertex3d(0.0, 0.0, 3.1415926535898); 

glVertex4f(2.3, 1.0, -2.2, 2.0); 

GLdouble dvect[3] = {5.0, 9.0, 1992.0};

glVertex3dv(dvect);

The first example represents a vertex with three-dimensional coordinates (2, 3, 0). (Remember that if it isn't specified, the z coordinate is understood to be 0.) The coordinates in the second example are (0.0, 0.0, 3.1415926535898) (double-precision floating-point numbers). The third example represents the vertex with three-dimensional coordinates (1.15, 0.5, -1.1). (Remember that the x, y, and z coordinates are eventually divided by the w coordinate.) In the final example, dvect is a pointer to an array of three double-precision floating-point numbers.

On some machines, the vector form of glVertex*() is more efficient, since only a single parameter needs to be passed to the graphics subsystem. Special hardware might be able to send a whole series of coordinates in a single batch. If your machine is like this, it's to your advantage to arrange your data so that the vertex coordinates are packed sequentially in memory. In this case, there may be some gain in performance by using the vertex array operations of OpenGL. (See "Vertex Arrays.")

OpenGL Geometric Drawing Primitives

Now that you've seen how to specify vertices, you still need to know how to tell OpenGL to create a set of points, a line, or a polygon from those vertices. To do this, you bracket each set of vertices between a call to glBegin() and a call to glEnd(). The argument passed to glBegin() determines what sort of geometric primitive is constructed from the vertices. For example, Example 2-3 specifies the vertices for the polygon shown in Figure 2-6.

Example 2-3 : Filled Polygon

glBegin(GL_POLYGON);

   glVertex2f(0.0, 0.0);

   glVertex2f(0.0, 3.0);

   glVertex2f(4.0, 3.0);

   glVertex2f(6.0, 1.5);

   glVertex2f(4.0, 0.0);

glEnd();

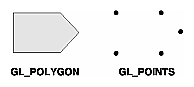
Figure 2-6 : Drawing a Polygon or a Set of Points

If you had used GL_POINTS instead of GL_POLYGON, the primitive would have been simply the five points shown in Figure 2-6. Table 2-2 in the following function summary for glBegin() lists the ten possible arguments and the corresponding type of primitive.

void glBegin(GLenum mode);

Marks the beginning of a vertex-data list that describes a geometric primitive. The type of primitive is indicated by mode, which can be any of the values shown in Table 2-2.

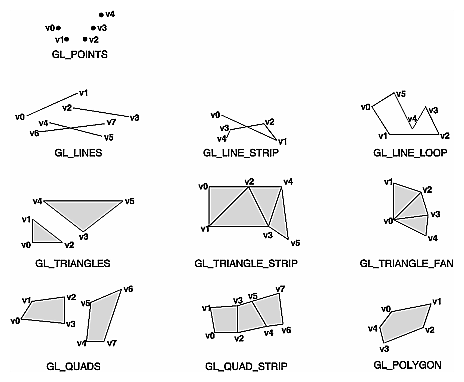
void glEnd(void);

Marks the end of a vertex-data list.

Figure 2-7 shows examples of all the geometric primitives listed in Table 2-2. The paragraphs that follow the figure describe the pixels that are drawn for each of the objects. Note that in addition to points, several types of lines and polygons are defined. Obviously, you can find many ways to draw the same primitive. The method you choose depends on your vertex data.

Figure 2-7 : Geometric Primitive Types

As you read the following descriptions, assume that n vertices (v0, v1, v2, … , vn-1) are described between a glBegin() and glEnd() pair.

Restrictions on Using glBegin() and glEnd()

The most important information about vertices is their coordinates, which are specified by the glVertex*() command. You can also supply additional vertex-specific data for each vertex - a color, a normal vector, texture coordinates, or any combination of these - using special commands. In addition, a few other commands are valid between a glBegin() and glEnd() pair. Table 2-3 contains a complete list of such valid commands.

No other OpenGL commands are valid between a glBegin() and glEnd() pair, and making most other OpenGL calls generates an error. Some vertex array commands, such as glEnableClientState() and glVertexPointer(), when called between glBegin() and glEnd(), have undefined behavior but do not necessarily generate an error. (Also, routines related to OpenGL, such as glX*() routines have undefined behavior between glBegin() and glEnd().) These cases should be avoided, and debugging them may be more difficult.

Note, however, that only OpenGL commands are restricted; you can certainly include other programming-language constructs (except for calls, such as the aforementioned glX*() routines). For example, Example 2-4 draws an outlined circle.

Example 2-4 : Other Constructs between glBegin() and glEnd()

#define PI 3.1415926535898 

GLint circle_points = 100; 

glBegin(GL_LINE_LOOP); 

for (i = 0; i < circle_points; i++) {   

   angle = 2*PI*i/circle_points;

   glVertex2f(cos(angle), sin(angle));

} 

glEnd();

Note: This example isn't the most efficient way to draw a circle, especially if you intend to do it repeatedly. The graphics commands used are typically very fast, but this code calculates an angle and calls the sin() and cos() routines for each vertex; in addition, there's the loop overhead. (Another way to calculate the vertices of a circle is to use a GLU routine; see "Quadrics: Rendering Spheres, Cylinders, and Disks" in Chapter 11.) If you need to draw lots of circles, calculate the coordinates of the vertices once and save them in an array and create a display list (see Chapter 7), or use vertex arrays to render them.

Unless they are being compiled into a display list, all glVertex*() commands should appear between some glBegin() and glEnd() combination. (If they appear elsewhere, they don't accomplish anything.) If they appear in a display list, they are executed only if they appear between a glBegin() and a glEnd(). (See Chapter 7 for more information about display lists.)

Although many commands are allowed between glBegin() and glEnd(), vertices are generated only when a glVertex*() command is issued. At the moment glVertex*() is called, OpenGL assigns the resulting vertex the current color, texture coordinates, normal vector information, and so on. To see this, look at the following code sequence. The first point is drawn in red, and the second and third ones in blue, despite the extra color commands.

glBegin(GL_POINTS); 

   glColor3f(0.0, 1.0, 0.0);                  /* green */

   glColor3f(1.0, 0.0, 0.0);                  /* red */

   glVertex(…);

   glColor3f(1.0, 1.0, 0.0);                  /* yellow */

   glColor3f(0.0, 0.0, 1.0);                  /* blue */

   glVertex(…);

   glVertex(…);

glEnd();

You can use any combination of the 24 versions of the glVertex*() command between glBegin() and glEnd(), although in real applications all the calls in any particular instance tend to be of the same form. If your vertex-data specification is consistent and repetitive (for example, glColor*, glVertex*, glColor*, glVertex*,…), you may enhance your program's performance by using vertex arrays. (See "Vertex Arrays.")