Transform2D ( const Matrix2D& matrix ) : m { matrix )
{
v.x = v.y = 0;
}
Transform2D& invert () {
m. invert (); v = m * v;
return *this;
}
Transform2D - getlnverse () const {
return Transform2D ( *this (.invert ();
}
// transform a point in space Vector2D 4transformPoint ( const Vector2D& p ) const {
return Vector2D ( v.x + m.x [Q][0]*p.x + + m.x [0][l]*p.y, v.y + m.x [1][0]*p.y + + m.x [1][l]*p.y );
}
// transform a direction // can change length Vector2D transformDir ( const Vector2D& p ) const { '
return Vector2D ( m.x [0][0]*p.x + m.x [0][l]*p.y,
m.x [1][0)*p.y + m.x [1][l]*p.y );
void buildHomogeneousMatrix ( float matrix [16] ) const;
const Vector2D& getTranslation () const {
return v;
}

const Matrix2D& getLinearPart () const return m;
static Transform2D getldentity ()
return Transform2D ( Matrix2D : : getldentityMatrix () ) ;
static Transform2D getTranslate ( const Vector2D& v )
return Transform2D ( Matrix2D ::
getldentityMatrix (), v );
static Transform2D getScale ( const Vector2D& s )
return Transform2D ( Matrix2D : : getScaleMatrix ( s ) ) ;
static Transform2D getScale ( float factor )
return Transform2D (Matrix2D ::
getScaleMatrix(Vector2D(factor, factor) )) ;
static Transform2D getRotate ( float angle )
return Transform2D ( Matrix2D ::
getRotateMatrix ( angle ) );
};

Аффинные преобразования в К3

Рассмотрим теперь аффинные преобразования в трехмерном пространстве. Как и ранее, рассмотрение начнем с основных видов преобразований -поворота, масштабирования, отражения и переноса.

Поворот

Преобразование поворота в общем случае задается при помощи матрицы Я , удовлетворяющей условию (1.7). Из этого соотношения вытекает

Д7?Г=/?ГЛ = /. (1.13)

Координаты и их преобразования

Несложно выписать матрицы поворота вокруг координатных осей. Матрица поворота вокруг оси Ох на угол <р имеет вид

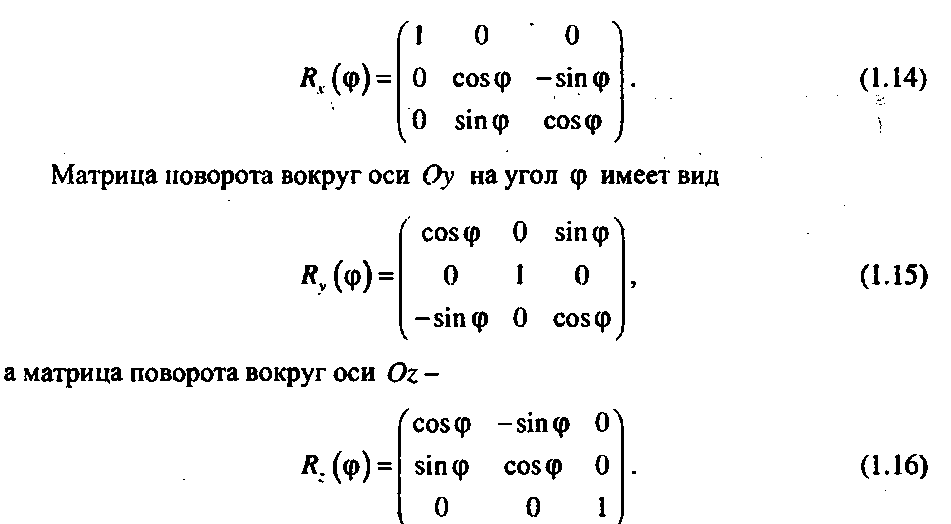
Поворот вокруг прямой, проходящей через начало координат и заданной направляющим вектором / на угол ср против направления часовой стрелки, можно представить в виде

⇐ Предыдущая| |Следующая ⇒