В этой главе мы рассмотрим работу с преобразованиями, в том числе и с преобразованиями координат. Также будут рассмотрены различные способы задания ориентации и проектирование.
Рассмотрим линейное пространство Ь над полем вещественных чисел (далее будем считать, что Ь = Л2 или Ь = Л3) и пусть задано отображение
(1.1)Определение. Отображение / называется линейным, если для всех вещественных А, и ц и всех векторов х, у е Ь выполняется следующее равенство (1.2):
/(Хг+цу) = #(*)+М/"(у)- (1.2)
Произвольное линейное преобразование (1.1) в /?2 можно представить в следующем виде: у = Мх, (1.3)
где М =
(1.4)матрица размера 2x2 из вещественных чисел.
Аналогично произвольное линейное преобразование в Къ задается матрицей 3x3:
'«II «12 «и'
М = пги тг2 т2} . (1.5) /Из, /Лз2 1Щ3
Преобразование (1.3) называется невырожденным, если определитель матрицы (1.4, 1.5) этого преобразования отличен от нуля (д&М * 0).
Основные преобразования в К
Рассмотрим сначала основные аффинные отображения в двухмерном пространстве.
Поворот
Поворот вокруг начала координат О (О,0) на угол ф против часовой стрелки (рис. 1.1) задается следующей формулой:
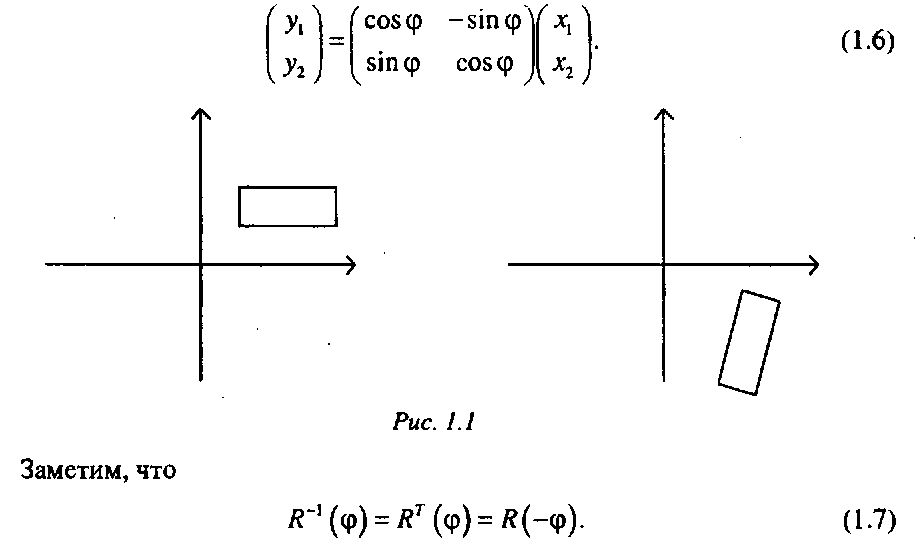
Обратите внимание, что определитель матрицы преобразования (1.6) равен единице. Таким образом, поворот - это невырожденное линейное преобразование.
Растяжение-сжатие (масштабирование)
Растяжение или сжатие вдоль координатных осей (рис. 1.2) задается следующей формулой:
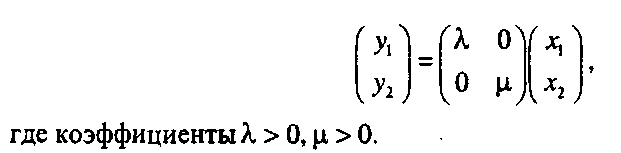
(1.8)Глава І. Координаты и их преобразования
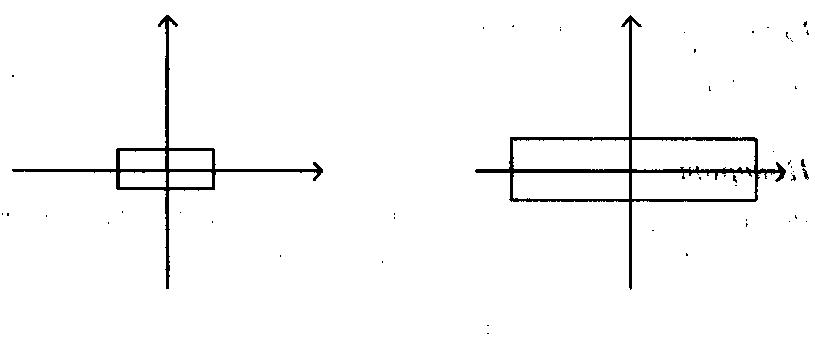
Рис. 1.2
В случае, когда А, > 1, ц > 1, происходит растяжение, а в случае X < 1, ц < 1- сжатие. Как видно из (1.8), это тоже линейное невырожденное преобразование (его определитель равен Хц).
Отражение Отражение относительно оси абсцисс (рис. 1.3) задается формулой
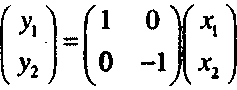
(1.9)Аналогично отражение относительно оси ординат задается формулой
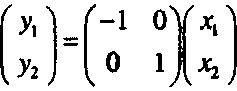
(1.10)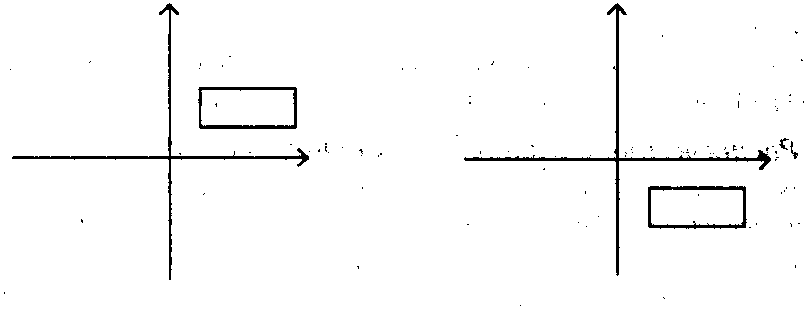
Рис. 1.3
Преобразование отражения (1.9, 1.10) также невырожденное линейное преобразование, его определитель равен -1.
