Однако приведенный код несет в себе определенную проблему - если позади зеркала или портала с преобразованием находятся какие-либо грани, то они могут оказаться видимыми сквозь зеркало (портал), так как в г-буфере они окажутся ближе, чем те грани, которые видны в нем.
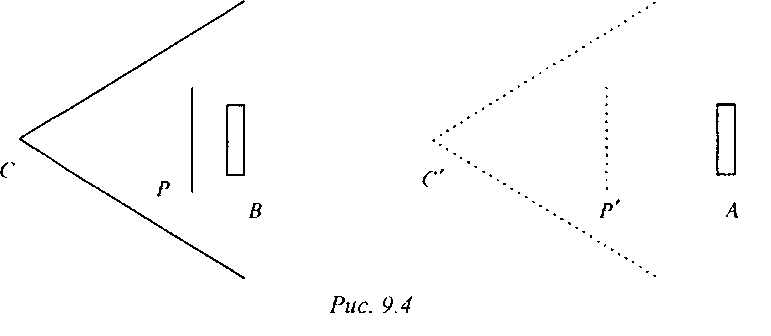
Как показано на рис. 9.4, объект В оказывается видимым и закрывает собой объект А, чего быть не должно (объект В вообще не должен быть виден для наблюдателя, расположенного в точке О.
Для решения данной проблемы достаточно выводить порталы и зеркала, за которыми могут находиться другие грани данной комнаты (их называют плавающими, floating) после вывода всех непрозрачных граней и чистить z-буфер (записывать в него значение, соответствующее максимальной глубине) за ними. При этом для корректной работы с полупрозрачными гранями те полупрозрачные грани, которые лежат за плавающим порталом (зеркалом), должны быть выведены перед ним.
Фактически это означает, что плавающие порталы и зеркала должны обрабатываться так же, как и обычные полупрозрачные грани. Тем самым для правильного упорядочение плавающих порталов (зеркал) и полупрозрачных граней можно использовать BSP-дерево.
Удобно сразу же при инициализации объекта SubScene пометить все плавающие объекты автоматически. Для этого внесем изменение в метод init класса SubScene. ci
intSubScene :: init () {
boundingBox.reset ();
for ( Array :: Iterator it = polys. getlterator ( ) ,-! it.end (); ++it )Пишем портальный рендерер (часть III)
{
Polygon3D * poly = (Polygon3D *) it.value () ,-
if ( poly -> testFlag ( PF_PORTAL ) | | poly -> testFlag ( PF_MIRROR ) ) if ( isFloating ( poly ) )
poly -> setFlag ( PF_FLOATING );
boundingBox. addVertices ( poly -> getVertices (),
poly -> getNumVertices () ) ;
}
return Object :: init ( ) ;
}Метод isFloating служит для проверки того, является ли данная грань (или портал) плавающей. Для этого достаточно проверить, есть ли хоть одна грань в данной комнате, лежащая позади данной. Для простоты мы будем классифицировать все порталы с преобразованием как плавающие.
