QuaternionSnormalize () ;
QuaternionSinitWithAngles ( float yaw, float pitch,
float roll ); Matrix3D getMatrix () const;
void getHomMatrix ( float * m ) const;
};Проектирование Важной операцией при работе с трехмерными объектами является проектирование.
Проектирование - это преобразование, ставящее точкам из пространства /?3 в соответствие точки на некоторой плоскости, называемой картинной.
В компьютерной графике используются два основных вида проектирования - параллельное и перспективное.
Глава І. Координаты и их преобразования Параллельное проектирование Рассмотрим плоскость п:(п,х) + с1 = 0 в пространстве /?3, на которую будет осуществляться проектирование.
Пусть также задан вектор /, вдоль которого будет осуществляться проектирование. При этом будем считать, что (Ли) Ф 0 .
Тогда для нахождения проекции произвольной точки д: на плоскость л проведем через точку л: прямую с направляющим вектором / и точку пересечения этой прямой с плоскостью л и назовем проекцией точки л: на плоскость л вдоль направления / (рис. 1.8).
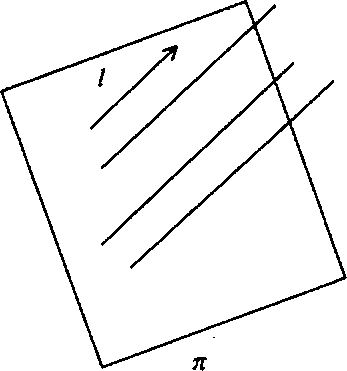
Рис. 1.8
Произвольная точка прямой, проходящей через точку д: и имеющей направляющий вектор /, имеет вид у = х + ТІ, (1.69)
где г є я.
Тогда параметр г точки пересечения этой прямой и плоскости л можно найти, подставив уравнение прямой (1.69) в уравнение плоскости
(х + Н,п) + с1 =0. (1.70)
Отсюда получаем с1 + (х,п)
1 = -7Г\- (171)
Зная г, легко находим проекцию точки х по формуле (1.69).
А. В. Боресков. Графит трехмерной компьютерной игры
Обратите внимание, что параллельное проектирование является аффинным преобразованием и поэтому его можно задать при помощи матрицы однородного преобразования.
Приведем матрицу канонического параллельного проектирования, осуществляемого на плоскость Оху вдоль оси Ог
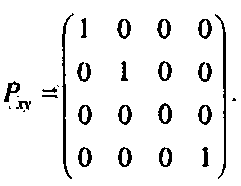
(1.72)Несмотря на свою простоту, параллельное проектирование обычно малоприменимо для визуализации сложных трехмерных сцен.
Перспективное проектирование Рассмотрим, как и ранее, картинную плоскость л: (л, х) + й = О. Пусть также задана точка с, которую будем называть центром проектирования. Тогда перспективной проекцией точки х назовем точку пересечения плоскости л с лучом, выходящим из с и проходящим через х при условии, что точка л: лежит в положительном полупространстве относительно плоскости л (рис. 1.9). Пусть проекцией точки х является точка у. Тогда, поскольку эта точка лежит на отрезке, соединяющем точки х и с, справедлива следующая формула:
