В противном случае ищутся такие ребра, для которых значения в концах будут разных знаков. Эти ребра пересекаются плоскостью к и соответствующие точки пересечения задают разбиение множества исходных вершин на множество вершин, лежащих в положительном полупространстве, и множество вершин, лежащих в отрицательном полупространстве, при этом сами точки разбиения войдут в оба этих множества.
Рассмотрим очередное ребро многоугольника (рис. 6.2).
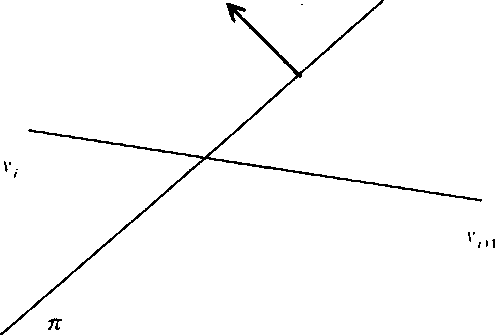
Рис. 6.2
Основные классы для рендерера. Работа с ресурсами
По отношению к плоскости тс может быть четыре различных случая (рис. 6.3).

Рис. 6.3
Тогда в случае а ребро целиком попадает в результирующий многоугольник, т. е. точка у,Ч1 добавляется к списку вершин усеченного многоугольника.
В случае б ребро пересекает плоскость лив усеченный многоугольник попадает только часть ребра от точки V, до точки у', и поэтому к списку
вершин добавляется точка пересечения \>'.
В случае в весь отрезок отсекается и в список вершин не попадает ни одной вершины из этого отрезка.
В случае г в список добавляется как точка пересечения V , так и точка .
Отрезок, соединяющий вершины v, и vlti, можно записать в параметрическом виде как
v = tv,+(l-0v1+I, (6.1)где параметр t принимает значения от 0 до 1.
Тогда для определения точки пересечения этого отрезка с плоскостью тс достаточно подставить уравнение (6.1) в уравнение плоскости и найти из него значение параметра.
/=f^4- (6.2)В результате этого определяются все вершины, задающие часть многоугольника, лежащую в положительном полупространстве. Аналогичным образом строится и часть многоугольника, лежащая в отрицательном полупространстве.
Еще одним методом является определение принадлежности точки. Данная операция осуществляется методом contains и достаточно подробно описана ранее.
Еще одним знакомым методом является определение пересечения многоугольника с заданным лучом. Это делается методом intersectByRay и также происходит аналогично описанному в гл. 3.
