В других трех треугольниках (исключая центральный) можно повторить описанную процедуру разбиения. Возвращаясь к узору Серпинского (см. рис. 2.4), вновь отметим, что и в средних треугольниках второго уровня разбиения точки узора не появляются.

Эти рассуждения лежат в основе второго варианта алгоритма построения узора Серпинского - варианта рекурсивного разбиения многоугольников. Этот алгоритм не требует генератора случайных чисел. Одно из достоинств второго варианта алгоритма состоит в том, что он позволяет использовать заливку многоугольников на экране. Стратегия построения узора довольно очевидна. Исходный треугольник делится на четыре, соединяя попарно середины прилежащих сторон, а затем средний треугольник изымается из дальнейших операций. Цикл повторяется с каждым из оставшихся трех треугольников до тех пор, пока размеры сформированных треугольников не станут достаточно малы - сравнимы с размерами пикселя.

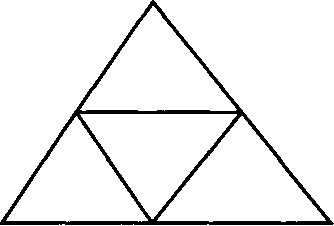
Рис 2.34. Один цикл разбиения треугольника

Графическое программирование

Этот процесс реализуется с помощью рекурсивно вызываемой функции, т.е. функции, вызывающей саму себя. Начинаем с построения исходного треугольника по трем заданным вершинам"opengl5_98.html">⇐ Предыдущая| |Следующая ⇒