Графическое программирование
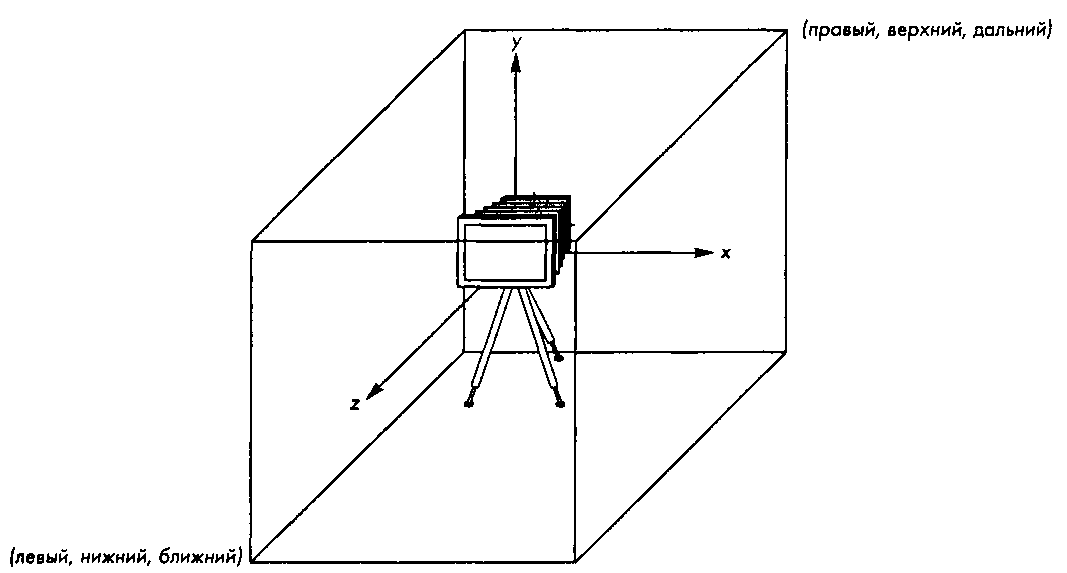
Рис. 2.31. Размещение камеры при настройке по умолчанию параметров параллелепипеда видимости при ортогональном проецировании. Показаны соответствие аргументов вызова функции д10гЬЬо() и положения вершин параллелепипеда
2.5.3. Матричный режим проецирования В системах компьютерной графики, использующих конвейерный принцип обработки, желательно, чтобы все операции формирования изображения выполнялись единообразно - в форме перемножения матриц. Ряд матриц преобразования являются переменными состояния системы OpenGL и действуют до тех пор, пока их принудительно не изменят. Из них наибольшее значение для нас сейчас имеют матрицы вида (model-view) и проецирования (или проективного преобразования). В начальном состоянии обе эти матрицы имеют вид единичных. В главе 4 читатели смогут познакомиться с имеющимися в составе OpenGL средствами выполнения операций с матрицами. Обычно этим матрицам присваиваются значения, которые отличают их от единичных. Специальные функции позволяют манипулировать любыми типами матриц. Выбор конкретного типа матрицы осуществляется настройкой переменной режима работы с матрицами (matrix mode). Эта переменная, как и ряд других, характеризует текущее состояние графической системы. По умолчанию переменной присваивается значение, соответствующее работе с матрицей вида (матрицы model-view). Поэтому для настройки типа проецирования нужно первым делом изменить состояние переменной режима работы с матрицами. Ниже приведен типовой фрагмент программы, в котором выполняется настройка двухмерного прямоугольника видимости.
glMatrixMode(GL_PR0JECTION); glLoadIdentity(J;
gluOrtho2D(0.0, 500.0, 0.0, 500.0); glMatrixMode(GL_MODELVIEW);Значения аргументов функции glu0rtho2D() задают прямоугольник видимости размером 500x500, левый нижний угол которого находится в начале двухмерной системы координат. Последний оператор фрагмента восстанавливается режим работы с матрицей вида. В сложной программе считается хорошим тоном восстанавливать значения параметров текущего со-
