С точки зрения алгоритмов заливки внутренней области недостаточно, чтобы многоугольник был простым. В некоторых API гарантируется правильное выполнение заливки только в случае, если многоугольник является выпуклым. Говорят, что геометрический объект является выпуклым (convex), если все точки отрезка, соединяющего две любые точки внутренней области объекта, также принадлежат внутренней области (рис. 2.12). Хотя в этой главе мы будем иметь дело только с двухмерными (плоскими) объектами, это определение справедливо и для трехмерных объектов. В число выпуклых объектов входят треугольники, тетраэдры, прямоугольники, круги, сферы и параллелеп""~цы (рис. 2.12). Существует множество алгоритмов проверки выпуклости объектов (см. упр. 2.20). Но следует отметить, что проверка выпуклости, как и проверка простоты многоугольника, требует достаточно сложных вычислений и, как правило, возлагается на прикладную программу.

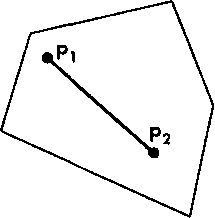
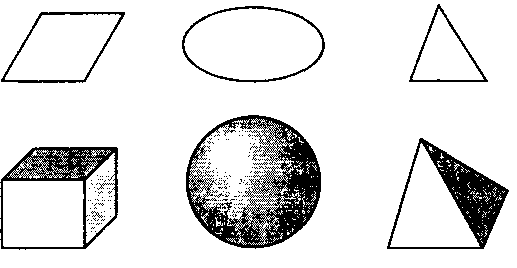
Рис. 2.12. К определению понятия "выпукюсти" Рис. 2.13. Выпуклые геометрические объекты
Графическое программирование
При работе с многоугольниками в трехмерном пространстве появляются дополнительные сложности. В этом случае многоугольник не обязательно является плоским, т.е. все его вершины не обязательно лежат в одной плоскости. Одна из геометрических теорем утверждает, что любые три неколлинеарные точки (т.е. точки, не лежащие на одной прямой) однозначно определяют плоскость, в которой лежит треугольник, построенный на этих трех вершинах. Этот вывод используется в большинстве графических систем. Следовательно, если использовать для аппроксимации криволинейных поверхностей только треугольники, то графическая система будет иметь дело исключительно с плоскими многоугольниками, которые всегда тонируются корректно. Кроме того, заливка треугольных областей выполняется аппаратно или программно значительно быстрее, чем заливка многоугольников другой формы.
2.3.2. Типы многоугольников в OpenGL
Теперь вернемся к типам объектов в OpenGL. Существует несколько типов плоских объектов, имеющих внутреннюю область (рис. 2.14).
