Поведение такой графической системы описывается двумя основными графическими функциями:
moveto(х,у); lineto(x,y); При выполнении функции moveto () перо приподымается и затем перемещается в точку с координатами (х,у), не оставляя следа на носителе (при этом траектория перемещения не имеет значения - главное, что заканчиваться она должна в точке с заданными координатами). При выполнении функции lineto() перо опускается и затем перемещается по прямой из текущего положения в точку с заданными координатами (х, у), оставляя след на носителе. Если добавить к этим функциям еще и функции настройки (выбор пера подходящего цвета и толщины), то получим законченную двухмерную графическую систему. Ниже приведен фрагмент программы вычерчивания несложного изображения с помощью такой системы:
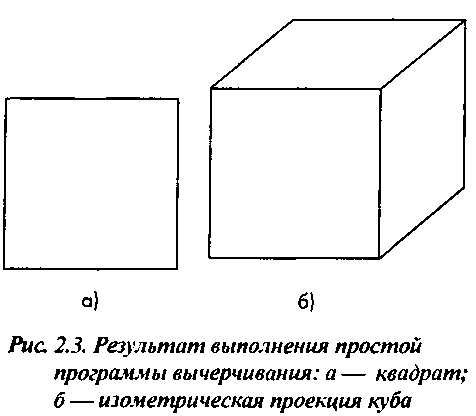
moveto(0, 0); lineto(l, 0); lineto(l, 1); lineto(0, 1); lineto(0, 0);Эта программа формирует изображение, представленное на рис. 2.3,а. Добавив в программу еще несколько операторов, получим при ее выполнении изображение куба в изометрической проекции (рис. 2.3,6).
moveto(0, 1); lineto(0.5, 1.866) lineto(1.5, 1.866) lineto(1.5, 0.866) lineto(l, 0); moveto(l, 1); lineto(l,5, 1.866)?В те не столь давние времена в русскоязычной литературе использовался термин "графопостроитель ". - Прим. перев.
2.1. Узор Серпинского
По этому принципу построены некоторые приложения, например системы компоновки страниц в полиграфии. Язык описания страниц PostScript является стандартным средством управления принтерами, в котором реализована эта же идея.
Но нас значительно больше интересует изображение трехмерных объектов. Модель перьевого плоттера не очень "вписывается" в процесс формирования изображений трехмерных объектов. Если, например, использовать эту модель для построения изображения трехмерного объекта на двухмерном планшете (то ли вручную, то ли с помощью компьютера), то в первую очередь нужно решить, где на планшете должна располагаться двухмерная точка, соответствующая определенной точке на изображаемом трехмерном объекте. Такие двухмерные точки являются, как было показано в главе 1, проекциями точек трехмерного пространства. Математически процесс формирования проекций описывается тригонометрическими соотношениями. Мы проанализируем эти соотношения в главе 5, но предпочтительнее использовать такой пакет API, который позволял бы пользователю формулировать свою задачу в терминах трехмерного пространства и не выполнять в прикладной программе никаких тригонометрических преобразований. Все операции, связанные с проективным преобразованием, должны взять на себя функции API. Такой подход очень удобен для пользователей, поскольку избавляет их от необходимости создавать доморощенные программы выполнения таких преобразований в составе своей прикладной системы. Пакет API, созданный профессионалами, решит эту задачу лучше и эффективнее.
