Единичная матрица I представляет собой квадратную матрицу, элементы главной диагонали которой равны 1, а остальные элементы равны 0:
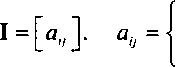
1, если / = j.
0 в противном случае.
Если матрицы А. В и I имеют одинаковые размеры, то выполняются соотношения А1 = А, 1В = В
В.З. Матрицы-строки и матрицы-столбцы
Особый интерес для задач компьютерной графики представляют матрицы-строки размера
1 х п и матрицы-столбцы размера их 1. Вектор и точку трехмерного пространства по отно шению к произвольному фрейму можно представить в виде матрицы-столбца: Р =
Для обозначения матриц-столбцов будем в дальнейшем использовать строчные буквы. Результатом транспонирования матрицы р будет матрица-строка Поскольку произведение матрицы размера п х / на матрицу размера 1хт представляет собой матрицу размера п х т, то произведение квадратной матрицы размера п на матрицу-столбец размера пх 1 даст новую матрицу-столбец размера пх 1. Стандартный способ геометрических преобразований в графических системах основан на использовании матриц-столбцов размером 2, 3 или 4 для представления точек или векторов и квадратных матриц для представления операторов преобразований. Следовательно, выражение р' = Ар
описывает отдельное преобразование точки (или вектора), а выражение р' = АВСр
описывает последовательность или суперпозицию преобразований. Обращаю ваше внимание на то, что поскольку операция умножения матриц обладает свойством ассоциативности, в этом выражении нет необходимости использовать скобки.
При использовании однородных координат, которые мы рассматривали в главе 4. векторы и точки представляются по-разному.
В.З. Матрицы-строки и матрицы-столбцы
В некоторых книгах по компьютерной графике авторы предпочитают описывать точки и векторы матрицами-строками. В таком случае, учитывая, что транспонирование произведения есть произведение транспонированных сомножителей в обратном порядке, т.е.
(АВ)Г=ВЛАГ, придем к выводу, что суперпозиция трех преобразований может быть записана для матрицы строки в следующем виде: р = р СБА.
Достоинство такой формы описания в том, что матрицы отдельных преобразований в комбинированном преобразовании перечисляются слева направо в том порядке, в котором элементарные преобразования реализуются в системе, т.е. сначала преобразование С, затем В, а потом А. Но в большинстве серьезных научных, технических и математических работ используется традиционная форма представления точек и векторов в виде матриц-столбцов. Поэтому и в данной книге мы отдали предпочтение этой форме. Хотя принципиального значения выбор той или иной формы и не имеет, при освоении нового АР1 обязательно обратите внимание, какая именно форма представления в нем использована, поскольку от этого зависит не только порядок перечисления матриц в составном выражении, но и сами матрицы преобразований должны быть транспонированы.
