12.5. Непосредственное отображение объема чества вычислительных операций, поскольку при любом изменении параметров наблюдателя необходимо полностью повторить все расчеты. Поэтому такой алгоритм не применяется в приложениях, предполагающих интенсивный диалог с пользователем.
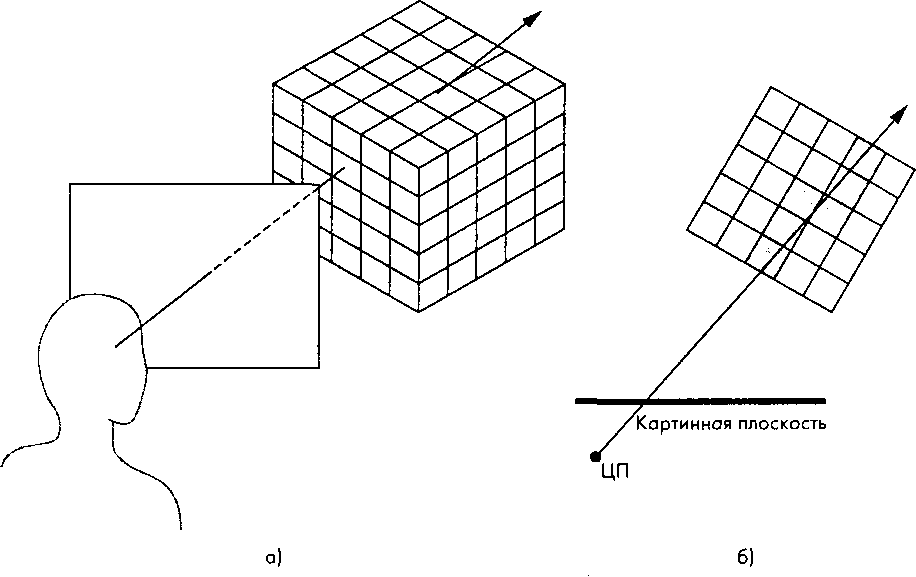
Рис. 12.26. Приведение лучей: а - трехмерный вид; б - вид сверху
12.5.4. Наложение текстуры на объем Технология наложения текстур играет весьма важную роль в приложениях, использующих анимацию, а потому современные графические системы комплектуются специальной памятью довольно большого объема для хранения и обработки текстур. Если наложение текстуры выполняется в основном на аппаратном уровне, то это практически не сказывается на скорости формирования окончательного изображения. Если же речь идет о программной реализации этого процесса, то в версию OpenGL 1.2 включены средства поддержки наложения трехмерных текстур.
Предположим, что в графической системе достаточно памяти для работы с текстурами, что позволяет разместить в ней весь массив данных скалярного поля. В таком случае можно определить множество плоскостей, параллельных картинной и рассекающих объем скалярного поля, и отобразить координаты текстуры на мировые координаты таким образом, что эти плоскости образуют множество параллельных многоугольников (рис. 12.27). После этого можно накладывать текстуры на образовавшиеся многоугольники. Поскольку количество многоугольников невелико- не более нескольких сотен, то процесс наложения текстур на них не слишком загрузит специализированные аппаратные средства. В отличие от других методов визуализации скалярных полей, метод с применением наложения текстур реализуется достаточно быстро, и его можно использовать в приложениях, ориентированных на интенсивный диалог с пользователем.
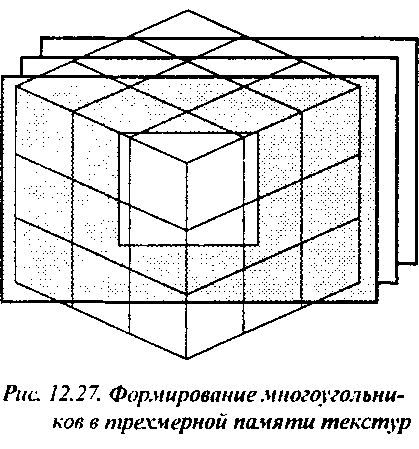
Визуализация данных научных исследований
12.6. Визуализация векторных полей Векторное поле отличается от скалярного тем, что в каждой его точке определено не отдельное значение, а «-мерный вектор. В результате имеем трехмерный объем, в каждой точке которого определена «-мерная вектор-функция f(x, у, z). Чаще всего исследуются трехмерные векторные поля, в которых каждая точка характеризуется трехмерным вектором. Примером может служить задача исследования распределения скоростей в потоке жидкости. При этом в каждой точке потока измеряется скорость - трехмерный вектор.
