void draw_one(int num, int i, int j, double a, double b, double c, double d)
{
/* пит = тип ячейки */
1*1, ] = индексы в массиве ячеек */
/* а, Ь, с, d = значения функции в четырех вершинах ячейки */
/* Б_Х, Б_у = ДЛИНЫ ребер ЯЧеЙКИ */
/* Здесь необходимо вычислить координаты левого нижнего угла ячейки по значениям индексов 1 и } */
{
case 1: case 14: xl=ox; yl=oy+s_y; x2=ox+s_x; y2=oy; break;/* Другие варианты */ }
/* Вычертить сегмент */
glBegin(GL_LINES);
glVertex2d(xl, yl);
glVertex2d(x2, y2); glEnd();
}Полный текст программы вы найдете в файле contour.с, который находится на ftp-сервере по адресу ftp.cs.unm.edu в каталоге /pub/angel/ВООК. На рис. 12.14 показаны две линии уровня для функции овалов Кассини
J[x, у) = [х2+у2+а2)2-Аа2х2-Ь4, рассчитанные при значениях сг=0,49 и Ь=0,5. В том изображении, которое показано на рисунке слева, использовался простейший вариант деления ребра ячейки пополам, а справа показано, как сглаживается линия уровня, если применяется линейная интерполяция. Функция была представлена массивом выборок размером 50 x 50. На рис. 12.15 показаны линии уровня (топографические горизонтали), построенные по данным топографической съемки острова Гонолулу в группе Гавайских островов.
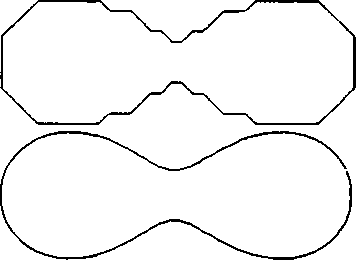
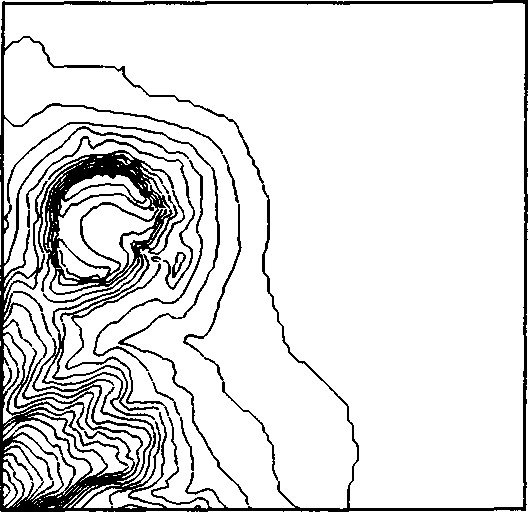
Рис. 12.14. Линии уровня овала Кассини: а - построенная с помощью алгоритма деления ребра пополам; б - построенная с помощью интерполяции выборок Рис. 12.15. Топографические горизонтали на карте острова Гонолулу
Существуют и другие методы построения линий уровня. Один из них состоит в том, что сначала отыскивается любая ячейка, через которую проходит линия, а затем отслеживается ее траектория, целенаправленным переходом из текущей ячейки в ту, куда "ушла" линия конту-
Визуализация данных научных исследований
pa. Этот метод кажется более производительным, поскольку анализируются не все ячейки подряд, а только те из них, через которые обязательно проходит линия уровня (раз уж она "нырнула" в ячейку, то обязательно должна из нее и "вынырнуть"), но он таит опасность упустить один из контуров линии уровня. Кроме того, достоинство рассмотренного выше метода в том, что анализ одной ячейки не зависит от другой, а следовательно, при наличии соответствующих средств ячейки можно анализировать параллельно. Кроме того, рассмотренный метод без особого труда переносится в трехмерное пространство, о чем вы узнаете в разделе 12.4. С некоторыми вариантами этого метода вы сможете познакомиться и в литературе, рекомендуемой в конце главы для самостоятельной проработки.
