Символы преобразуются в графические объекты в результате интерпретации сформированных строк, причем для этого могут быть использованы разные способы. Один из подходов базируется на графической системе черепашьей графики' (turtle graphics) (см. упр. 2.4). В
2В отечественной литературе по отношению к этому способу формирования штриховых графических объектов иногда используется термин "паучья графика ". - Прим ред.
Процедурные методы
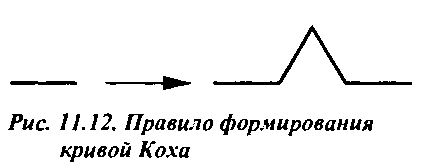
этой графической системе образ объекта формируется в результате манипуляций с перемещением графического курсора- черепахи, который оставляет след на поле изображения. Есть три главные команды управления черепахой - ее можно передвинуть вперед на 1 единицу, повернуть вправо или влево. Угол поворота фиксирован (но в каждой частной системе может иметь место свое значение - например, 30°, 45°, 90° и т.п.). Обозначим три базовые операции символами F, R и L. Любая строка таких символов имеет простую и очевидную графическую интерпретацию. Если, например, в системе используется угол поворота 120°, то интерпретация строки FRFRFR приведет к формированию равностороннего треугольника. Добавим в набор символов еще два: /- для обозначения операции записи состояния черепахи (ее положения и ориентации) в стек, a J - для операции восстановления состояния, извлеченного из стека. Пусть графическая система настроена на угол поворота 60°. Рассмотрим порождающее правило
F -» FLFRRFLF,графическая интерпретация которого показана на рис. 11.12. Если применить это правило повторно ко всем символам F в новой строке, то получим кривую, показанную на рис. 11.13, а, после повторного применения к этой кривой- замкнутую кривую, показанную на рис. 11.13, б. Эти кривые известны в научном мире под именами собственными кривой Коха (Koch curve) и снежинки Коха (Koch snowßake) и являются примерами так называемых заполняющих кривых (space-filling curves): при рекурсивном применении правила кривая растягивается все больше и больше, но при этом нигде не пересекает саму себя. Если на каждом шаге рекурсии уменьшать масштаб условной единицы длины при геометрической интерпретации, то кривая, несмотря на увеличение суммарной длины траектории, будет все время "вписываться" в определенную прямоугольную оболочку.
