Предположим, что имеется множество вершин, определяющих графические примитивы, из которых формируется изображение. Поскольку все объекты представлены в терминах координат положения точек в пространстве, можно рассматривать множество типов примитивов и вершин как геометрические данные. Сложная сцена описывается тысячами, если не миллионами, вершин. Все их нужно обработать по одному алгоритму и в результате сформировать в буфере кадра описание растра. Если рассматривать этот процесс в терминах геометрических операций с исходными данными, то можно представить его в виде схемы рис. 1.29. На этой схеме показаны четыре основных этапа процесса:
геометрическое преобразование;
отсечение;
проективное преобразование;
растровое преобразование.
1.8. Архитектура графических систем
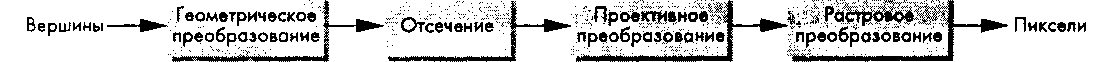
Рис. 1.29. Структура геометрического конвейера В последующих разделах мы обсудим детали реализации каждого из этих этапов. Но главный вывод, который следует из всего изложенного, состоит в том, что если для всех объектов сцены выполняются единообразные преобразования, то быстрее всего можно реализовать этот процесс с помощью специализированного процессора с конвейерной архитектурой.
Большинство этапов обработки графической информации можно описать в форме геометрических преобразований представления объектов сцены в разных системах координат. Например, рассматривая модель синтезированной камеры, приходим к выводу, что основная часть процесса визуализации представляет собой преобразование представления объектов из базовой (мировой) системы координат в систему координат камеры. Другой пример - стадия размещения изображения на поле экрана ЭЛТ или другого устройства вывода. Внутреннее представление геометрических объектов - будь то в системе координат камеры или в любой другой подходящей системе координат, используемой в графическом API,- должно быть преобразовано на этой стадии в представление в системе координат устройства отображения. Каждое такое преобразование можно представить в матричной форме, причем последовательные преобразования выражаются перемножением (конкатенацией - concatenating) соответствующих матриц элементарных преобразований. В результате формируется матрица комплексного преобразования. В главе 4 будет подробно рассмотрен математический аппарат описания геометрических преобразований. Поскольку произведение двух матриц есть также матрица, этот математический метод является прекрасным кандидатом для реализации в форме конвейерных вычислений. Кроме того, поскольку матрицы преобразований в компьютерной графике имеют небольшие размеры (4x4), сам процесс умножения матриц также можно распараллелить в блоке, который выполняет эту операцию.
