р7Ар+Ь7р+с = О, где
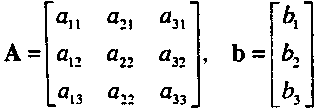
Кривые и криволинейные поверхности
Десять независимых коэффициентов в А, Ь и с определяют конкретный вид квадратичной поверхности. Однако для классификации можно воспользоваться последовательностью преобразований поворота и сдвига, в результате которой частная поверхность будет приведена к каноническому (стандартному) виду. В трехмерном пространстве такие преобразования можно представить в виде р' = Мр+с1.
Матрица М представляет собой матрицу поворота, которая преобразует А в диагональную матрицу 0=М7АМ. Например, уравнение эллипсоида в каноническом виде выглядит так: Все коэффициенты в этом уравнении положительны. Обращаю ваше внимание на то, что поскольку при приведении уравнений поверхностей к каноническому виду используются аффинные преобразования, то свойства квадратичных поверхностей сохраняются такими преобразованиями, что хорошо сочетается со свойствами примитивов других типов.
10.11.2. Вычисление точек на квадратичной поверхности методом приведения лучей Вычислить координаты точек на квадратичной поверхности в процессе формирования ее изображения можно с помощью метода приведения лучей. Представим в параметрической форме луч, исходящий из точки ро в направлении <1: р = р0+а<1.
Подставляя его в уравнение квадратичной поверхности, получим скалярное уравнение относительно переменной а: а2(17А(1+а(17(Ь+2Аро)+ро'Аро+Ь7(1+с = 0.
Это уравнение может не иметь ни одного действительного корня, один или два действительных корня. Результат решения уравнения можно использовать либо для заполнения буфера кадра, либо как промежуточный результат при выполнении тонирования по методу трассировки лучей. Кроме того, можно к любой точке квадратичной поверхности применить стандартный алгоритм закрашивания, поскольку, располагая аналитическим выражением поверхности, несложно вычислить компоненты нормали: Такой метод построения может быть распространен на все виды алгебраических поверхностей. Пусть имеется уравнение поверхности в виде
<7(р) = <7(х,.у, г) = 0.
