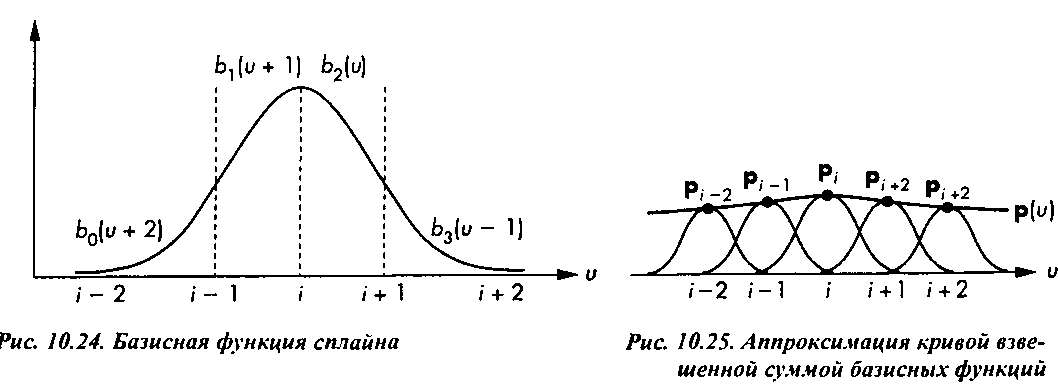
10.7.3. Сплайновые поверхности В-сплайновая поверхность является таким же расширением В-сплайновых кривых, как поверхность Безье является расширением кривых Безье. Используя функции смешивания В-сплайновых кривых, получим уже знакомое вам описание порции поверхности: р(^)=х£г>>)^0')р,,.

Отличие его от аналогичного соотношения для поверхности Безье заключается в том, что оно справедливо только для порции, расположенной около центрального четырехугольника массива опорных точек (рис. 10.26). На расчет поверхности, соответствующей всему массиву опорных

точек, уйдет в 9 раз больше времени, чем в случае Безье-поверхности. Но зато на том же множестве опорных точек удается построить гораздо более плавную поверхность, чем при использовании формы Безье.

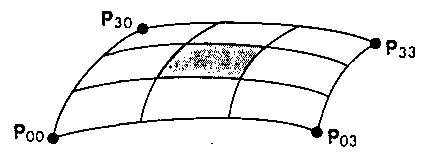
Рис. 10.26. Порция сплайновой поверхности

10.8. Обобщенные В-сплайны

Предположим, что имеется ансамбль опорных точек ро,--, рт В общем виде задача аппроксимации формулируется как поиск функции р(и)=[х(и) у(и) z{u)]', определенной на интервале umin <и< umèx, которая является достаточно гладкой и проходит в определенном смысле достаточно близко к опорным точкам. Предположим, что имеется множество значений {ик}, называемых узлами (knots), такое, что

"min = U0<U\< … < U„ = Umtx.

Кривые и криволинейные поверхности

Последовательность щ, их,…, и„ будем называть массивом узлов12. При использовании аппроксимации сплайнами функция р(и) имеет вид полинома степени d на интервале между соседними узлами"opengl5_489.html">⇐ Предыдущая| |Следующая ⇒