8.9.2. Бинарные деревья разделения пространства Деревья, представляющие графы сцен и объекты в конструктивной геометрии тел, описывают иерархические отношения между компонентами объектов. Эти деревья можно использовать для описания мирового пространства объектов и инкапсулировать в них пространственные отношения между группами объектов. Один из подходов к представлению пространственной иерархии объектов основан на том очевидном факте, что плоскость разделяет пространство на две части - два подпространства. Полученные подпространства можно затем делить плоскостями на подпространства все меньших размеров. Наглядно это можно представить в двухмерном случае, когда пространство - двухмерная плоскость - делится прямыми.
Рассмотрим многоугольники и наблюдателя, показанных на рис. 8.24.
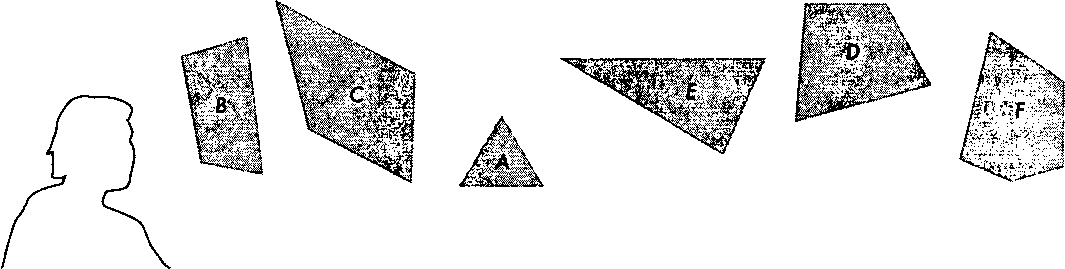
Рис. 8.24. Наблюдатель и множество многоугольников Как мы показали в главе 7, существует такой порядок включения образов многоугольников в суммарное изображение сцены, который обеспечивает последовательное перекрытие образов одних многоугольников другими, и в результате создается корректное изображение всей совокупности. Эту идею можно реализовать не только с помощью метода сортировки, но и с помощью дерева, представляющего пространственные отношения между многоугольниками в совокупности4. Процесс формирования дерева начинается с разделения пространства сцены плоскостью одного из многоугольников, причем, какого именно, принципиального значения не имеет. В результате такого разбиения все многоугольники оказываются разделены на две группы - одни принадлежат тому полупространству, которое находится перед разделяющей плоскостью, а другие принадлежат полупространству, которое находится за По сути, это тоже один из видов сортировки. - Прим. ред
Иерархические графические модели
разделяющей плоскостью. Например, рассмотрим простую сцену, в которой все многоугольники параллельны и ориентированы таким образом, что их нормали направлены вдоль оси г. Это предположение не влияет на общность метода, а только упрощает его понимание и графическое представление. Если многоугольники не параллельны и разделяющая плоскость пересекает какие-либо из них, то последние разбиваются на два многоугольника, один из которых включается в первую группу, а второй - во вторую. Вид на такое пространство со стороны координатной оси у показан на рис. 8.25.
