Появление ступенек объясняется тремя причинами. Во-первых, объем буфера кадра, в котором формируется дискретизированный образ графического объекта, конечен, и представление в нем прямолинейного отрезка в принципе не является взаимно однозначным, т.е. одному и тому же растровому образу может соответствовать множество исходных отрезков. Во-вторых, все пиксели имеют строго фиксированное положение на экране и образуют сетку с постоянным шагом. В-третьих, пиксели имеют фиксированный размер и форму.
На первый взгляд кажется, что, поскольку все эти причины органически присуши дискретному способу представления непрерывного сигнала, вряд ли что-нибудь удастся сделать и что отмеченные погрешности изображения неустранимы. Алгоритмы, подобные предложенному Брезенхэмом, оптимальны в том смысле, что позволяют определить на дискретной сетке позиции, ближайшие к исходной линии. Но если конструкция устройства отображения позволяет воспроизводить оттенки цветов или даже градации одного цвета, эффект ступенчатости изображения можно значительно ослабить. Как известно, линия как математический объект является одномерным многообразием- характеризуется только длиной, но не имеет ширины (толщины). В отличие от исходного математического объекта, его растровый образ имеет конечную ширину, иначе он просто не был бы различим визуально. Каждый пиксель, из которых этот образ состоит, имеет вполне определенные размеры - размер пикселя принят в наших рассужде-
Алгоритмы формирования изображения
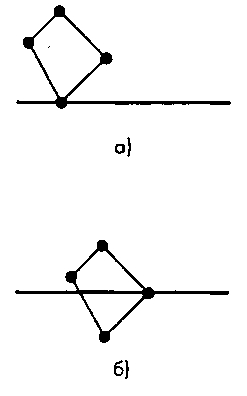
ниях за некую метрическую единицу. Поэтому можно считать, что идеализированный образ математической прямой линии на экране имеет толщину 1 единицу (рис. 7.58). Вычертить на экране растрового устройства отображения такой идеальный образ прямой невозможно, поскольку он не состоит из отдельных квадратных пикселей. Алгоритм Брезенхэма можно считать способом приближенного представления этого идеального образа на сетке из реальных пикселей. Если присмотреться к идеальному образу прямой, то нетрудно подметить, что многие пиксели он перекрывает частично. В "чистом" виде алгоритм Брезенхэма предполагает, что при коэффициенте наклона, меньшем 1, за каждый шаг перемещения по оси х засвечивается точно один пиксель. Но можно поступить и по-другому - засвечивать и те пиксели, которые частично перекрываются идеальным образом линии, но задавать им не полную интенсивность, а частичную, приблизительно пропорциональную степени перекрытия пикселя. В результате сформируется сглаженное изображение прямой, примерно такое, как на рис. 7.59,6. Этот способ получил название сглаживание усреднением по области (antialiasing by area averaging). Для реализации такого способа необходимо выполнить операции, весьма схожие с теми, которые выполняются при отсечении многоугольника. Существуют и другие алгоритмы сглаживания ступеней на изображении, которые применяются при отображении примитивов других типов, в частности многоугольников.
