Закрашиваемые участки строки определяются в результате анализа точек пересечения линии строки и контура многоугольника. Вся информация, необходимая для определения точек
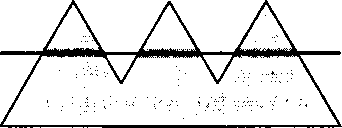
Рис. 7.53. Строка растра, пересекающая многоугольник
Алгоритмы формирования изображения
пересечения, содержится в списке вершин, и порядок выявления этих точек зависит от порядка следования вершин в списке представления многоугольника. Рассмотрим, например, многоугольник, представленный упорядоченным списком вершин (рис. 7.54). Само собой напрашивается решение формировать точки пересечения строк растра с ребрами многоугольника в порядке описания ребер в списке вершин. Номера точек пересечения на рис. 7.54 показывают порядок их вычисления при последовательном просмотре ребер. Весь процесс вычислений можно сформулировать в приращениях (см. упр. 7.18). Но для выполнения закраски внутренней области многоугольника такой порядок следования точек пересечения не годится (или, по крайней мере, очень неудобен). Если в каждом цикле алгоритма нужно формировать участок закраски на одной строке, то необходимо рассортировать точки пересечения в порядке следования соответствующих строк, а затем - по значению координаты х на каждой строке, как показано на рис. 7.55. Очевидное решение - отсортировать список точек пересечения после того, как он будет сформирован в процессе последовательного анализа ребер, - не приемлем, поскольку при обработке многоугольника сложной формы (с "зубцами") количество точек пересечения п может оказаться очень большим и сортировка займет много времени. Если, например, многоугольник пересекает примерно половину строк растра, то оценка сложности сортировки имеет вид 0(п \ogn) и для реализации в реальном масштабе времени такой способ явно не годится.
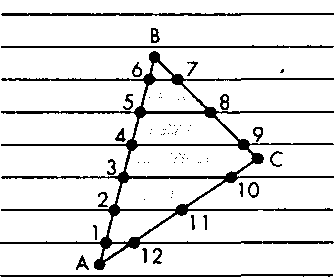
Рис. 7.54. Порядок следования точек пересечения при последовательной обработке ребер многоугольника
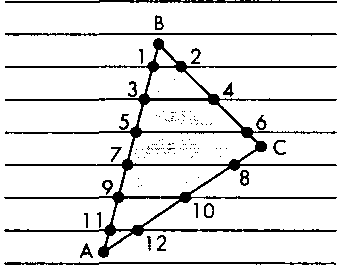
Рис. 7.55. Желательный порядок следования точек пересечения Существует множество способов, позволяющих обойтись без глобальной сортировки списка точек пересечения. Один из них, получивший название у-х алгоритма (у-х algorithm), предусматривает формирование отдельного подсписка для каждой строки. По мере обработки ребер многоугольника информация о каждой очередной точке пересечения помещается в соответствующий подсписок, причем процедура включения нового элемента в подсписок сразу выполняет его упорядочение по значению координаты х. В результате формируется структура данных, показанная схематически на рис. 7.56. Здесь вы видите еще один пример того, как продуманная организация структуры данных повышает скорость выполнения операций в графической системе.
