если на предыдущем шаге произошло приращение у, то
= ак-т + 1, Ьш = Ьк + т-\, Ьк+\-ам = (Ьк-ак) + 2т-2; в противном случае
= ок-т, Ьк+\ = Ьк + т, Ьк+\-ак+х = (Ьк-ак) + 2т.
Умножив полученные выражения на Ах, получим, что при переходе к следующему значению х значение а\ изменяется либо на 2Ау, либо на 2(Ду-Ах). Этот результат можно записать в таком виде:
!2Ау, если а*к < 0;
2(Ду - Ах) - в противном случае.
В результате вычисление каждого очередного пикселя растрового образа отрезка потребует только одной операции сложения целых чисел и анализа знака. Алгоритм настолько эффективен, что в СБИС он реализован в виде одной инструкции. Метод вычисления исходного значения с/0 я предлагаю читателям разработать самостоятельно (см. упр. 7.14).
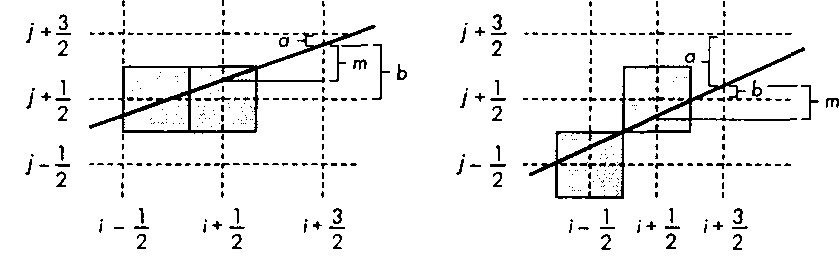
Рис 7.45. Приращение значений параметров а и Ь
7.10. Растровое преобразование многоугольников Одним из главных преимуществ первых растровых систем отображения перед векторными была возможность формировать изображения областей со сплошной закраской. В те не столь уж давние времена было невозможно в реальном времени сформировать оттенки цвета отдельных пикселей области, а потому термин растровое преобразование многоугольника означал формирование его образа с заливкой внутренней области одним цветом. В отличие от растрового преобразования отрезков, которое практически во всех графических системах реализуется одним и тем же алгоритмом, для растрового преобразования многоугольников
7.10. Растровое преобразование многоугольников существует множество методов, причем отдать предпочтение какому-либо одному довольно сложно. Выбор во многом зависит от архитектуры графической системы, и мы сосредоточим внимание на тех методах, которые совместимы с конвейерной архитектурой и способны поддерживать тонирование внутренней области многоугольника разными оттенками цвета. Обзор прочих методов будет сделан в разделах 7.10.4-7.10.6.
7.10.1. Тест принадлежности внутренней области Внутренняя область простого плоского многоугольника определяется однозначно, если многоугольник выпуклый. Он корректно отображается в любой графической системе, в том числе и в OpenGL. Но иногда приходится включать в изображение и многоугольники общего вида, для которых с первого взгляда трудно сказать, что же именно следует считать его внутренней областью. Если все вершины многоугольника не лежат в одной плоскости, то приходится работать с его проекциями (см. раздел 7.10.2) или использовать для формирования внутренней области плоскость, определяемую первыми тремя вершинами этого многоугольника. Для многоугольников, имеющих пересекающиеся ребра (самопересекающихся многоугольников), нужно сформулировать правило принятия решения, как определять принадлежность точки внутренней области такого многоугольника. Концептуально задача заполнения внутренней области многоугольника определенным цветом или трафаретом сводится к задаче определения принадлежности точки его внутренней области.
