Ачгоритмы формирования изображения
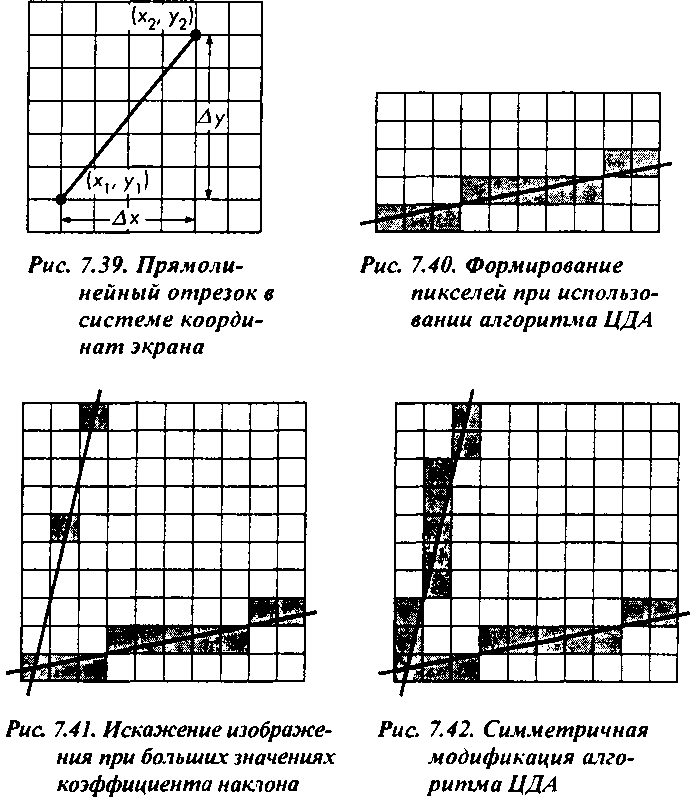
ролями" - задаваясь значениями координаты^ отображающей точки, будем определять подходящее значение координаты х (рис. 7.42). Заодно обращаю ваше внимание на то, что использование такой симметричной модификации алгоритма устраняет потенциальные проблемы с горизонтальными и вертикальными отрезками. Попытайтесь самостоятельно сформулировать варианты этого же алгоритма для отрицательных значений коэффициента наклона.
Поскольку прямолинейный отрезок определяется вершинами, то при назначении кода цвета каждому очередному пикселю можно также использовать интерполяцию, но не пространственных координат, а "цветовых". Кроме того, в процессе интерполяции отрезка можно, управляя цветом, накладывать на образ отрезка штрихи, точки и т.п. Все эти дополнительные эффекты не рассматриваются как часть алгоритма растрового преобразования, но часто реализуются синхронно с ним.
7.9. Алгоритм Брезенхэма Описанный алгоритм ЦДЛ при всей его простоте и наглядности обладает одним недостатком- при формировании координат каждой отображающей точки необходимо выполнять сложение действительных чисел. Более простой целочисленный алгоритм предложил Брезенхэм (ВгеБеппат) в 1965 году, и с тех пор этот алгоритм используется практически во всех графических системах, причем существуют как программные, так и аппаратные его реализации.
Как и при анализе алгоритма ЦДА, будем считать, что конечные точки отрезка представлены целочисленными координатами (хъу\) и (х2,у2), а коэффициент наклона удовлетворяет условию 0 < т < 1.
7.9. Алгоритм Брезенхэма Это условие достаточно критично для работоспособности алгоритма. Суть алгоритма в том, что при построении растрового образа отрезка выбирается пиксель, ближайший по вертикали к соответствующей прямой. Рассмотрим промежуточный шаг растрового преобразования отрезка после того, как будет сформирован пиксель (/ + 1/2,7 + 1/2) (рис. 7.43). Известно, что прямая описывается уравнением у = тх + И.
При х = / + 1/2 прямая проходит от центра пикселя - точки с координатами (/'+ 1/2,у'+ 1/2)- не далее, чем на 1/2 шага между пикселями12. В противном случае образ прямой вследствие округления не прошел бы через этот пиксель. При переходе к следующей точке, для которой х = / + 3/2, учитывая ограничения, наложенные на значение коэффициента наклона, образ отрезка должен пройти либо через пиксель с центром в (/ + 3/2,у' + 1/2), либо через пиксель с центром в (/' + 3/2, j + 3/2).
