другого, и выявить такую ситуацию позволит индивидуальный анализ всех вершин одного из многоугольников (см. упр. 7.12).
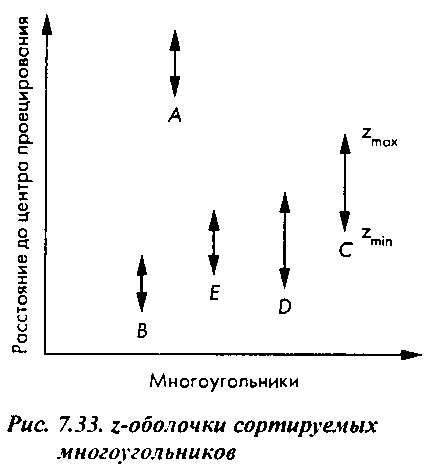
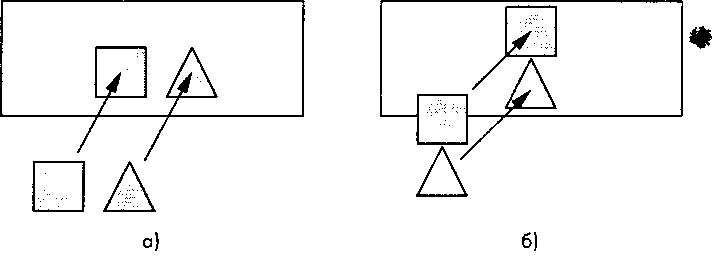
Рис. 7.34. Анализ перекрытия х- и у-оболочек многоугольников: а - х-оболочки не перекрываются; б - у-оболочки не перекрываются Но остаются еще две ситуации, с которыми справиться особенно трудно.
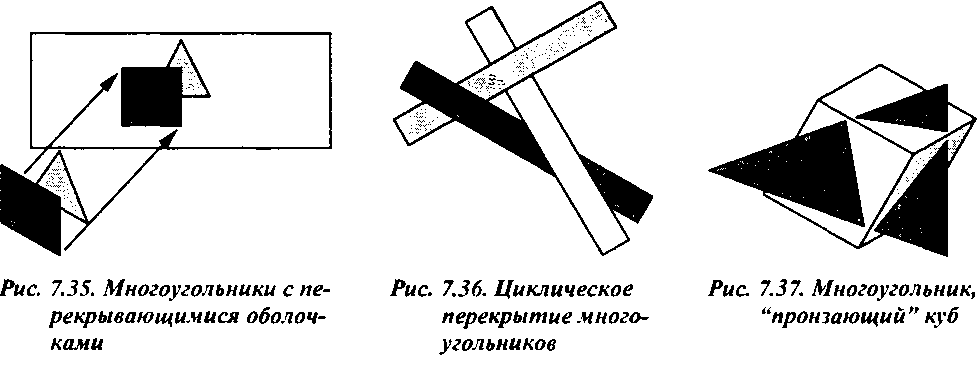
Во-первых, три многоугольника могут перекрывать друг друга циклически, как показано на рис. 7.36. В таком случае вообще не существует такого порядка формирования образов многоугольников, который позволил бы получить корректное изображение. Лучшее, что
^Сравнивать х- и у-оболочки можно только при параллельном проецировании. Здесь мы опять встречаемся с доводом в пользу предварительной перспективной нормализации.
7.7. Удаление невидимых поверхностей можно предложить, - разделить по крайней мере один из них на две части и попытаться повторить анализ образовавшегося набора из четырех многоугольников.
Во-вторых, возможна ситуация, когда один многоугольник "пронзает" другой (или другие), как показано на рис. 7.37. В такой ситуации придется детально проанализировать пересечение, используя обобщенные методы отсечения одного многоугольника общего вида другим аналогичным многоугольником. Если пересекающиеся многоугольники имеют много вершин, можно попытаться использовать какие-либо искусственные методы, учитывающие специфику ситуации и требующие меньшего объема вычислений.
Оценить производительность метода сортировки по глубине очень сложно, поскольку многое зависит от специфики приложения. Например, работая с многоугольниками, представляющими собой грани сплошных объемных объектов, мы заранее знаем, что многоугольники не могут пересекаться. Но как бы там ни было, необходимость в предварительной сортировке явно указывает на то, что оценка производительности, как функции от сложности отображаемой сцены, не может быть линейной.
7.7.4. Алгоритм построчного сканирования В те не столь уж давние времена, когда память стоила довольно дорого и о специализированных БИС для создания графических систем с конвейерной архитектурой только мечтали, метод построШьго сканирования считался наиболее эффективным алгоритмом удаления невидимых поверхностей. И по сей день отдельные идеи этого метода применяются в специализированных системах. Алгоритм построчного сканирования сочетает удаление невидимых поверхностей с растровым преобразованием. Хотя детальное обсуждение растрового преобразования еще ждет нас в последующих разделах, основные идеи этого алгоритма мы можем рассмотреть, воспользовавшись рис. 7.38. На этом чертеже вы видите два многоугольника, пересекающихся в пространстве. При растровом преобразовании многоугольников, которое выполняется последовательно, строка за строкой, можно воспользоваться методом вычисления глубины в приращениях, рассмотренным ранее. Но присмотревшись к этому чертежу внимательнее, можно отыскать еще более эффективный способ обработки. Перемещаясь вдоль строки растра \, мы пересекаем ребро а многоугольника А. Поскольку это первый многоугольник, который пересекается строкой, нет смысла выполнять какие-либо вычисления, анализирующие его глубину. Начиная с этого пикселя, последующим присваивается код цвета, соответствующий окраске многоугольника А. Но когда по мере перемещения по строке мы встретимся со следующим ребром этого многоугольника, Ь, то это будет означать, что с обработкой многоугольника А на этой строке покончено и можно присваивать последующим пикселям код цвета фона. Так будет продолжаться до тех пор, пока не встретится ребро с многоугольника В; поскольку перед этим на строке отображался фон, можно опять не при-
