Пусть сцена состоит из k трехмерных непрозрачных многоугольников, каждый из которых можно считать независимым объектом. Обобщенный подход, основанный на анализе пространства объектов, предполагает попарное сравнение положения всех объектов по отношению к наблюдателю (центру проецирования). Рассмотрим два таких объекта: многоугольники А и В. Существует четыре варианта их взаимного положения (рис. 7.27):
А полностью закрывает В - в изображение нужно включить только А;
В полностью закрывает А - в изображение нужно включить только В;
А и В не перекрываются - в изображение нужно включить оба объекта, А и В;
7.7. Удаление невидимых поверхностей
А и В частично перекрываются - нужно вычислить, какая часть перекрываемого многоугольника будет видима наблюдателю.
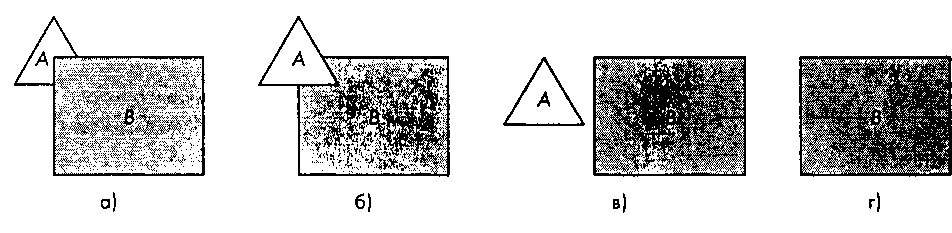
Рис. 7.27. Два многоугольника: а- В частично закрывает А; б- А частично закрывает В; в - А и В не перекрываются; г - В полностью закрывает А
Для того чтобы оценить сложность процесса, будем считать, что анализ, какой вариант сочетания многоугольников имеет место для текущей пары, и вычисление видимой части многоугольника представляют собой единую операцию. Будем обрабатывать множество имеющихся в сцене объектов итеративно. Берем один из к многоугольников и попарно сравниваем его с каждым из оставшихся к-\ многоугольников. После выполнения этого цикла будет известно, какая часть выбранного многоугольника будет видима наблюдателю (если таковая вообще существует). Закончив с анализом одного многоугольника, перейдем к следующему, который точно так же будем попарно сравнивать с оставшимися к-2 многоугольниками. Такой итерационный цикл продолжается до тех пор, пока не останутся только два многоугольника, которые мы и сравним в последнем итерационном цикле. Несложно показать, что оценка сложности всего процесса имеет вид 0{к2). Следовательно, даже не вдаваясь в детали выполнения операций сравнения, можно прийти к выводу, что объектно-ориентированный подход лучше всего применять при отображении сцен, состоящих из относительно небольшого количества объектов.
