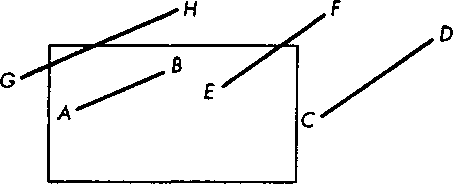
Суть задачи отсечения двухмерных отрезков поясняется на рис. 7.5. Предположим, что уже выполнено проецирование и в нашем распоряжении имеется двухмерное описание изображения в картинной плоскости. На этой же плоскости определена и рамка отсечения, которая соответствует видовому окну на экране дисплея. Все параметры заданы вещественными числами. Как видно на рисунке, отрезок АВ полностью попадает на экран, а ни один из участков отрезка СО не попадает. Отрезки ЕР и ОН нужно укоротить перед тем, как выводить на экран. Хотя отрезок прямой однозначно описывается координатами крайних точек, на примере отрезка ЄН вы можете убедиться, что, хотя крайние точки отрезка и лежат вне зоны видимости, часть отрезка все-таки может попадать в эту зону.
ство операций умножения и деления заменены операциями сложения и вычитания действительных чисел и побитовыми логическими операциями булевой алгебры.
Выполнение алгоритма начинается с продления сторон рамки отсечения в обе стороны до бесконечности, в результате чего картинная плоскость делится на девять областей (рис. 7.6). Каждой области присваивается четырехразрядный двоичный номер - характеристический код (ошсоа'е)- ЬффгЬъ, который формируется следующим образом. Пусть (х,у)- координаты некоторой точки на картинной плоскости. Тогда
7.3.1. Алгоритм Коэна-Сазерленда Рис. 7.5. Двухмерное отсечение
Можно вычислить координаты точек пересечения прямой с рамкой видимости и использовать эту информацию для отсечения, но весь-то фокус в том и состоит, чтобы по возможности минимизировать объем вычислений и обойтись без определения точек пересечения, которое непременно включает операцию деления чисел с плавающей точкой. Исторически первым, отвечающим этим требованиям, был алгоритм Коэна-Сазерленда (Cohen-Sutherland algorithm), в котором большин-
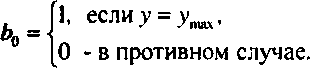
Алгоритмы формирования изображения
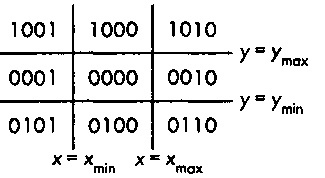
Рис. 7.6. Характеристические коды областей картинной плоскости Аналогично, 6| приравнивается 1, если у < ymin, а значения Ь2 и Ь3 определяются отношением между компонентой х и абсциссами левой и правой границ рамки отсечения. В результате девяти областям присваиваются коды, представленные на рис. 7.6. При анализе отрезка первым делом определяется, в каких областях находятся его конечные точки, и им присваиваются соответствующие характеристические коды. Эта процедура требует выполнения восьми операций вычитания на каждый отрезок.
