}Полагая, что источники света уже сформированы в программе и что работа с ними разрешена, внесем изменения в функцию triangle(), которые позволят сформировать изображение закрашенного треугольника: void triangle( point3 a, point3 b, point3 с) {
point3 n;
cross(a, b, c, n); glBegin(GL_P0LYG0N);
glNormal3fv(n);
glVertex3fv(a);
glVertex3fv(b);
glVertex3fv(c); glEnd();
}В результате программа сформирует изображение аппроксимированной сферы, представленное на рис. 6.39. Обратите внимание на то, что на контуре изображения сферы отчетливо виден излом между соседними многоугольниками аппроксимирующего многогранника.
Перейти от этой программы к варианту, использующему интерполяционное закрашивание, можно довольно просто, поскольку для сферы известно направление нормали в каждой точке р - нормаль должна быть направлена вдоль радиуса, а в нашем частном случае - от начала координат к точке р. После этого с каждой вершиной аппроксимирующего многогранника можно связать нормаль именно к поверхности сферы, a OpenGL будет в процессе закрашивания выполнять интерполяцию между вершинами каждого треугольника. Таким образом, нам понадобится скорректировать текст функции triangle () следующим образом:
void triangle( point3 a, point3 b, point3 с) {
point3 n; int i;
glBegin(GL_P0LYG0N);
for(i=0;i<3;i++) n[i]=a[i]; normal(n); glNormal3fv(n); glVertex3fv(a); for(i=0;i<3;i++) n[i]=b[i];6.9. Закрашивание модели сферы
normal(n); glNormal3fv(n); glVertex3fv(b); for(i=0;i<3;i++) n[i]=c[i]; normal(n); glNormal3fv(n); glVertex3fv(c); glEnd();
}Результат закрашивания, полученный при выполнении этого варианта программы, показан на рис. 6.40.
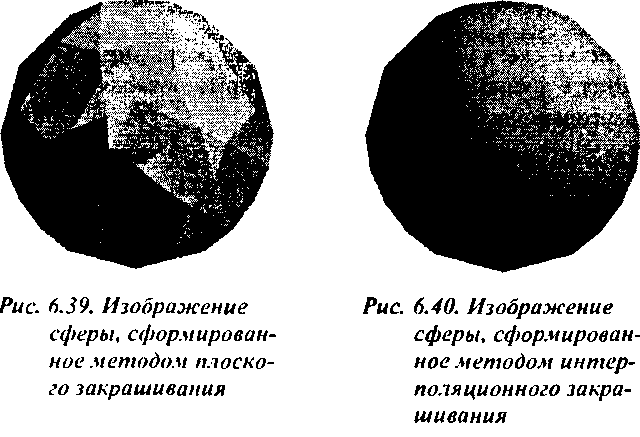
Но, к сожалению, такой метод определения нормали можно применять только при работе с поверхностями, которые описываются довольно простыми аналитическими зависимостями. При формировании изображения в этом варианте программы не использовался метод Гуро, иначе пришлось бы при формировании каждой вершины вычислять нормали всех пересекающихся в ней граней. В программе не создается структура данных, отражающая топологию аппроксимирующего многогранника, а потому в ней отсутствует необходимая для метода Гуро информация. Попробуйте выполнить упр. 6.9 и 6.10, в которых предлагается сформировать необходимую структуру данных. Обратите внимание на то, что в аппроксимирующем многограннике, полученном по методу половинного деления, в каждой вершине пересекаются шесть граней, в то время как в исходном тетраэдре - три.
