Правюьный икосаэдр имеет 12 граней, каждая из которых является равносторонним треугольником. Такой многогранник прекрасно подходит для аппроксимации сферы; см [Оре97,а].
6.6. Аппроксимация сферической поверхности рекурсивным разбиением воспользуемся методом, который применялся при формировании узора Серпинского в главе 2, - разделим каждую сторону треугольника пополам и соединим средние точки, как показано на рис. 6.35, в.
После того как каждая грань будет разделена выбранным способом, четыре новых треугольника будут лежать в плоскости прежней грани. Поэтому нам придется сдвинуть новые вершины на поверхность аппроксимируемой сферы, выполнив нормализацию их координат. Эта операция реализуется приведенной ниже программой:
void normal(point3 р) {
double d=0.0; int i;
for(i=0; i<3; i++) d+=p[i]*p[i]; d=sqrt(d);
if(d > 0.0) for(i=0; i<2; i++) p[i)/=d;
}Таким образом, разбиение треугольника, заданного вершинами с индексами a, b и с, может быть выполнено с помощью следующей программы:
point3 vl, v2, v3; int j;
for(j=0; j<3; vl[j]=v[a][j]+v[b][j];
normal(vl);
for(j=0; j<3; j++) v2[j]=v[a][j]+v[c][j]; normal(v2);
for(j=0; j<3; j++) v3[j]=v[c][j]+v[b][j]; normal(v3);
triangle(v[a], v2, vl); triangle(v[c], v3, v2); triangle(v[b], vl, v3); triangle(vl, v2, v3);Этот код можно использовать в подпрограмме формирования тетраэдра и с его помощью сформировать 16 треугольных граней вместо прежних четырех. Но желательно повторить подобную процедуру п раз, получая после каждого цикла все более близкое приближение многогранника к сфере. Рекурсивно вызывая подпрограмму разбиения, мы можем контролировать количество циклов, а через него - точность аппроксимации.
Первое, что нам придется для этого сделать, - модифицировать подпрограмму формирования тетраэдра и ввести в нее аргумент номера цикла п, который задает глубину рекурсии:
void tetrahedron(int n) {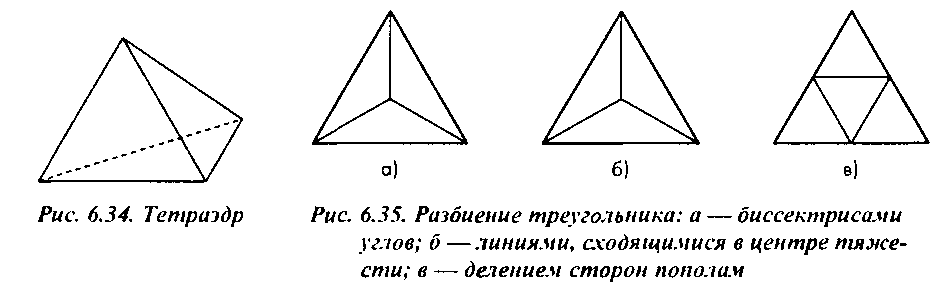
Закрашивание
divide_triangle(v[0], v[l], v[2], n); divide_triangle(v[3], v[2], v[l], n ) divide_triangle(v[0], v[3], v[l], n ) divide_triangle(v[0], v[2], v[3], n ) }