Мы рассматривали модель Фонга в пространстве объектов, но в графической системе тонирование изображения выполняется после того, как описания объектов будут преобразованы посредством матриц вида и проецирования. Эти преобразования могут изменить члены, включающие функцию косинуса (см. упр. 6.22). Следовательно, чтобы получить правильный результат, придется либо каким-то образом сохранить используемые пространственные соотношения после выполнения геометрических преобразований объектов, либо в процессе тонирования выполнять необходимые обратные преобразования.
/s = AsZ.s(r-v)a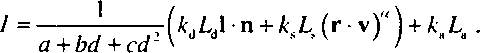
Закрашивание
6.4. Вычисление векторов Описанная модель отражения света объектами сцены никак не связана с видом проецирования (параллельным или перспективным) и является достаточно общей в том смысле, что может применяться как к плоским, так и к криволинейным поверхностям, причем расстояние между поверхностью и наблюдателем не имеет значения. Большая часть вычислений в процессе тонирования изображения пространственной сцены приходится на определение компонентов векторов, используемых в модели Фонга, и их скалярных произведений. В процессе выполнения этих вычислений часто используются разнообразные упрощения, учитывающие специфику конкретной ситуации. Например, если анализируемая поверхность - плоский многоугольник, то для всех ее точек вектор нормали будет одним и тем же. Если источник света удален от поверхности достаточно далеко, то для всех точек этой поверхности вектор 1, характеризующий направление падения лучей от этого источника, будет одним и тем же.
В этом разделе мы рассмотрим методы вычисления компонентов векторов для общего случая, а в разделе 6.5 проанализируем возможные упрощения в частных случаях, когда поверхности отображаемых объектов можно представить совокупностью плоских многоугольников. Этот частный случай представляет для нас особый интерес, поскольку в большинстве графических систем, в том числе и в OpenGL, при выполнении тонирования криволинейные поверхности аппроксимируются множеством малых плоских многоугольников.
