Фонг предложил приближенную модель, в которой учет зеркальною отражения очень незначительно увеличивает объем вычислений по сравнению с моделью, учитывающей только диффузное отражение. В этой модели вводится дополнительный аддитивный член, учитывающий зеркальное отражение. Таким образом, поверхность представляется шероховатой для составляющей диффузного отражения и гладкой - для составляющей зеркального отражения. Интенсивность светового потока, который достигает наблюдателя, зависит от угла ф между вектором г, характеризующим направление идеального зеркального отражения, и вектором v, направленным к наблюдателю. В модели Фонга используется уравнение

/, = £Дсо8аф.

Коэффициент £s (0 < kt < 1) определяет, какая часть светового потока отражается. Показатель степени а - это коэффициент резкости бликов (shininess coefficient). Ha рис. 6.19 показано, как при увеличении значения а отраженный свет концентрируется в зоне, близкой к углу идеального зеркального отражения. В пределе, при возрастании а до бесконечности, получим идеальное зеркало; значения в диапазоне от 100 до 500 соответствуют характеру отражения от большинства металлических поверхностей, а малые значения (<100) соответствуют наиболее распространенным материалам с обычными оптическими свойствами.

Рис. 6.18. Зеркальная поверхность

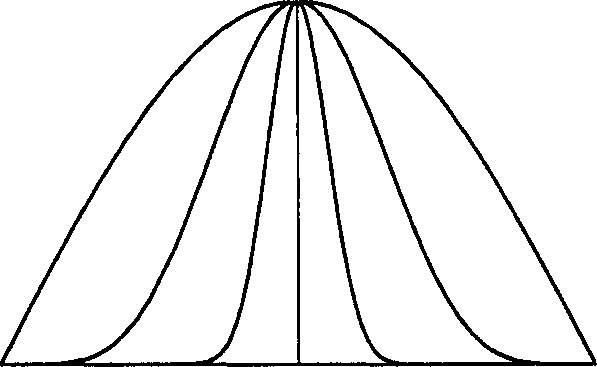
Рис. 6.19. Эффект изменения коэффициента резкости бликов

6.3. Модель отражения Фонга Располагая данными о нормализованных векторах г и п, можно использовать в модели Фонга операцию скалярного произведения и таким образом несколько сократить объем вычислений. В этом случае член, учитывающий зеркальное отражение, принимает вид В это выражение можно добавить множитель, учитывающий расстояние до источника света, который имеет такой же вид, как и в выражении для диффузного отражения. В результате получим выражение для модели Фонга {Phong model), учитывающей это расстояние"opengl5_278.html">⇐ Предыдущая| |Следующая ⇒