В компьютерной графической модели в роли глаза наблюдателя выступает картинная плоскость (рис. 6.3) и изображение формируют только те лучи, которые достигли центра проецирования, пройдя внутри зоны, ограниченной рамкой отсечения картинной плоскости. Обратите внимание на то, что большинство лучей, испускаемых источником, не попадает на картинную плоскость, а потому не представляет для нас никакого интереса. Мы воспользуемся этим выводом позже, в разделе 6.10. Будем считать, что картинная плоскость разделена на прямоугольники, каждому из которых соответствует отдельный пиксель экрана, причем цвет пикселя зависит от цвета луча, попавшего на этот пиксель.
На рис. 6.2 показаны варианты и однократного, и многократного взаимодействия луча с объектами. Именно характер этого взаимодействия и определяет, что же увидит наблюдатель- красный объект или коричневый, темный или светлый, матовый или блестящий.
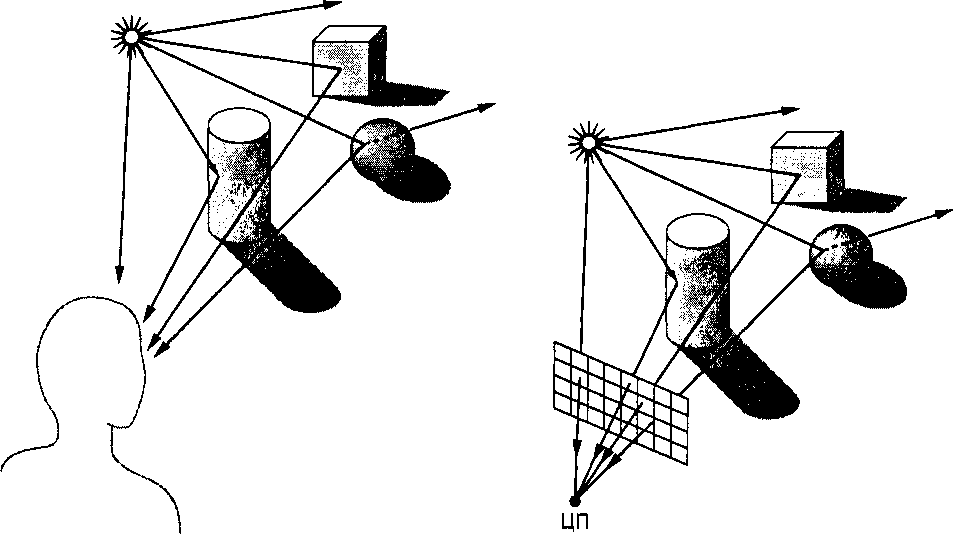
Рис. 6.2. Свет и поверхности Рис. 6.3. Световые лучи, поверхности объектов и изображение на экране компьютера
6.1. Свет и материя Когда луч попадает на поверхность, часть его энергии поглощается, а часть - отражается. Если поверхность непрозрачна, то вся энергия луча распределяется между процессами отражения и поглощения. Если же поверхность прозрачна, то часть энергии луча проходит через эту поверхность и может взаимодействовать с другими объектами. Характер взаимодействия зависит от длины световой волны. Объект, облученный белым светом, кажется наблюдателю красным, потому что большая часть энергии падающего света поглощена материалом объекта, а та, что отразилась, имеет максимум интенсивности в красной части спектра. Объект кажется наблюдателю блестящим, если его поверхность гладкая. И наоборот, объект, поверхность которого шероховата, кажется наблюдателю матовым. Распределение теней на поверхности объекта зависит также от ориентации отдельных участков его поверхности, т.е. от направления вектора нормали в каждой точке этой поверхности. Можно выделить три основных типа характера взаимодействия света и материала поверхности (рис. 6.4).
