Для того чтобы сформировать в изображении тени (или, как сказал бы художник, наложить тени), нужно представлять себе физику процесса взаимодействия света и материалов реальных объектов. Об этом мы подробно поговорим в главе 6. А в этом разделе только покажем, насколько сложна подобная задача из-за объема вычислений, которые при отображении динамических объектов должны выполняться в реальном масштабе времени.
Но как бы там ни было, без формирования теней нельзя обойтись при воссоздании в компьютере изображения, близкого к реальному, а потому в тех системах, где требуется еще и высокая динамика изображения, приходится идти на различные хитрости. Рассмотрим, как образуется тень при использовании единственного точечного источника света (рис. 5.41). Для простоты предположим, что тень падает на плоскую поверхность у = 0. При этом на поверхности образуется многоугольник тени (shadow polygon), который является ничем иным, как проекцией объекта-многоугольника на заданную поверхность, причем центр проецирования располагается в той точке, где находится источник света. Таким образом, если удастся сформировать проекцию исходного объекта-многоугольника во фрейме, начало координат которого совпадает с источником света, то получим вершины многоугольника тени. Далее нужно сформировать представление полученных вершин в мировой системе координат. Эту задачу
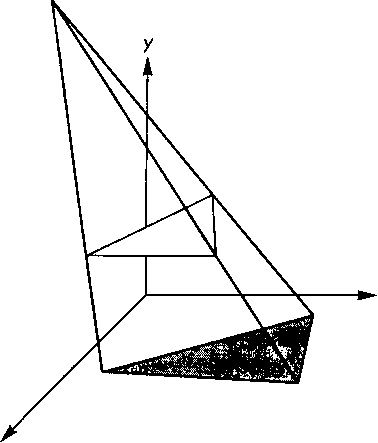
Рис 5.41. Тень от отдельного многоугольника
Визуализация
можно решать в прикладной программе, но гораздо рациональнее подобрать подходящую матрицу проективного преобразования и передать дальнейшие заботы о формировании многоугольника тени графической системе, в данном случае -OpenGL. Предположим, что источник света находится в точке (х/, y/t zt), как показано на рис. 5.41.
Если с помощью матрицы сдвига T(-xt, -yh -z,) изменить положение объектов на рисунке таким образом, чтобы источник света оказался в центре координат (рис. 5.42,6), то получим обычную перспективную проекцию с центром проецирования в начале координат. Матрица проективного преобразования при этом имеет вид
