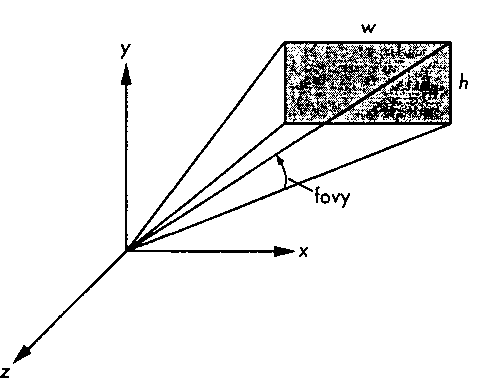
Рис. 5.27. Задание пирамиды видимости с помощью углов зрения
5.4.2. Параллельное проецирование в OpenGL
В составе OpenGL имеется только одна функция для задания параметров параллельного проецирования, которая формирует ортогональную проекцию:
glOrtho(xmin, xmax, ymin, ymax, near, far)Аргументы вызова этой функции имеют тот же геометрический смысл, что и одноименные аргументы функции glFrustum( ). Зона видимости при этом превращается в параллелепипед видимости (рис. 5.28.). Как и в случае перспективной проекции, передняя отсекающая плоскость описывается уравнением z = rmin = -/„, где /„ - значение аргумента near, а задняя отсекающая плоскость - уравнением z = rmax = -//, где //- значение аргумента far.
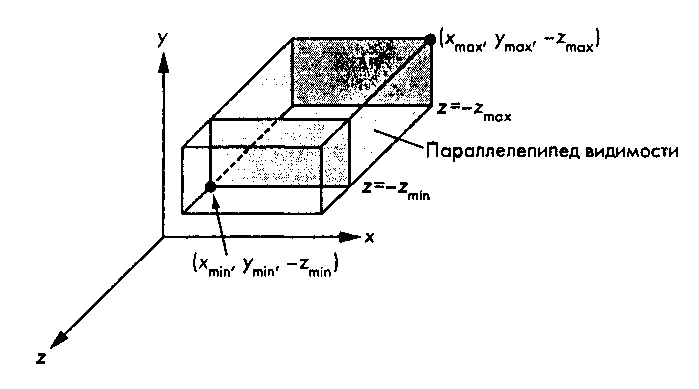
Рис. 5.28. Параметры ортогональной проекции При формировании перспективной проекции расстояния до передней и задней плоскостей отсечения должны были быть положительными, поскольку все проецирующие лучи должны были пересекаться в центре проецирования. Поэтому объекты, расположенные "за" центром проецирования, будут изображаться "вверх ногами". Точки на плоскости z = 0 вообще не могут быть спроецированы, поскольку это приведет к делению на нуль. При параллельном проецировании все эти проблемы отпадают, а потому ограничение на знаки расстояний до плоскостей отсечения при вызове функции gl0rtho() снимаются. Остается единственное ограничение -far > near.
Визуализация
5.5. Удаление невидимых поверхностей Теперь можно вернуться к программе вращения куба, которую мы рассматривали в главе 4, и добавить в нее перспективную визуализацию и перемещение камеры. Но сначала выясним, как выполняется удаление невидимых поверхностей, - этот процесс мы использовали в первой версии программы без объяснения. Когда мы смотрим на объект, в данном случае куб, грани которого непрозрачны, то видим только три ближайшие к нам грани. Принимая во внимание используемую модель визуализации, это можно объяснить тем, что проецирующие лучи, исходящие из центра проецирования, блокируются этими гранями и не могут достичь точек на других гранях.
