V = TR.Вектор v должен быть ортогонален вектору п, следовательно, n v = 0.
5.2. Размещение камеры
На рис. 5.16 видно, что v является проекцией на картинную плоскость, заданную своей нормалью п. Следовательно, v есть линейная комбинация п и лу:
V = осп + (3\у.
Если пренебречь длинами векторов, то можно положить (3=1 и получить
\У п
. а =-п п и
v = \у--п .
п п Теперь можно определить третий вектор правой тройки как векторное произведение: и = v x п.
В общем случае эти векторы не являются единичными, поэтому их нужно нормализовать и получить три единичных вектора (орта) осей координат фрейма камеры и', v1 и п'. Матрица поворота
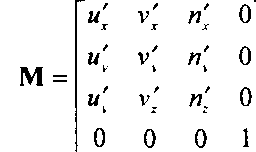
позволяет получить ориентацию вектора, заданного в системе и', v1, п', по отношению к осям координат исходной системы. Но нам нужно решать обратную задачу - получить представление вектора, заданного в исходной системе координат,, в системе и', v1, п'. Поэтому нужно обратить матрицу М, но поскольку это матрица "чистого" поворота, то обращение можно заменить транспонированием: К = М-1 = мг.
Последняя операция - умножение на матрицу сдвига Т:
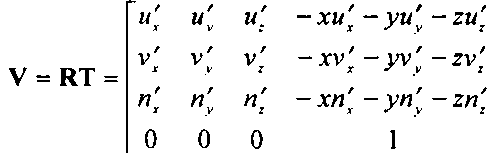
Обратите внимание на то, что в данном случае матрица сдвига стоит в произведении справа, в то время как раньше мы умножали ее слева. Интерпретировать это отличие можно следующим образом: в первом случае мы сначала поворачивали фрейм, а затем отодвигали его в направлении, которое было представлено в координатах фрейма камеры. В данном же случае позиция камеры (а следовательно, и требуемое ее смещение из исходного положения) представлена в координатах мирового фрейма.
Можно и по-другому разобраться в этих отличиях. Обратите внимание на то, что матрицы ИТ и ТК имеют аналогичную структуру. Ориентирующие части обоих произведений матриц - верхние левые подматрицы 3x3 - идентичны, а три первых элемента четвертого столбца отличаются по той простой причине, что компоненты смещения выражаются в них в разных фреймах. В произведении ТК - это компоненты в неповернутом фрейме, а в произ-
Визуализация
ведении КТ - в повернутом. Для примера с получением изометрического вида, который был рассмотрен в предыдущем разделе, имеем:
