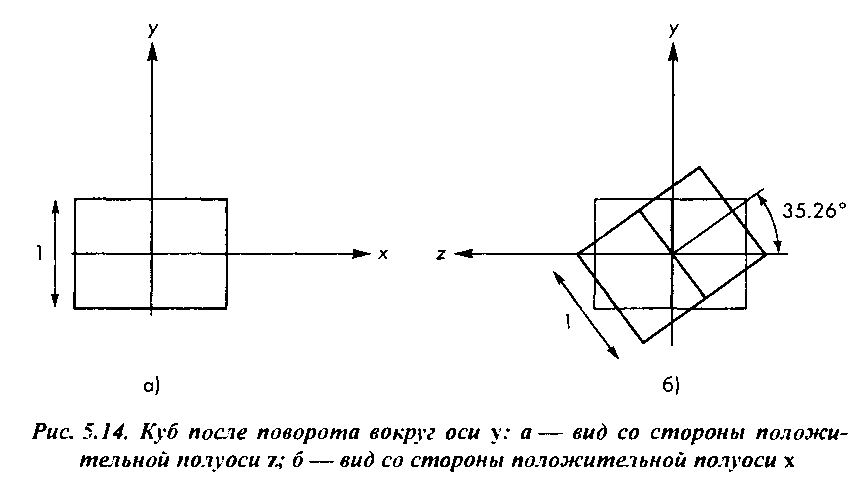
Рассмотрим, какое положение занял куб после первого поворота. Поскольку мы смотрим на него со стороны положительной полуоси г, то куб будет выглядеть, как на рис. 5.14,а.
Вершина (-1, 1, 1) теперь займет положение (0, 1, 42). Если теперь посмотреть на куб со стороны оси х, как на рис. 5.14,6, то очевидно, что нужно поворачивать его до тех пор, пока правая верхняя вершина не совместится с осью у. Прямоугольный треугольник, который содержит этот угол, имеет катеты 1 и 42 , что соответствует углу 35.26°. Поворот должен быть выполнен по часовой стрелке, а значит, нужно взять этот угол со знаком "минус". Последний шаг - отодвинуть камеру от начала координат. Следовательно, наша стратегия - сначала повернуть фрейм камеры относительно фрейма объекта, а затем разделить два фрейма. Соответствующая матрица вида определяется следующим образом: м = ТК^.
Элементы этой матрицы вычисляются суперпозицией матриц элементарных преобразований в однородных координатах. Перемножение матриц поворотов дает следующее:
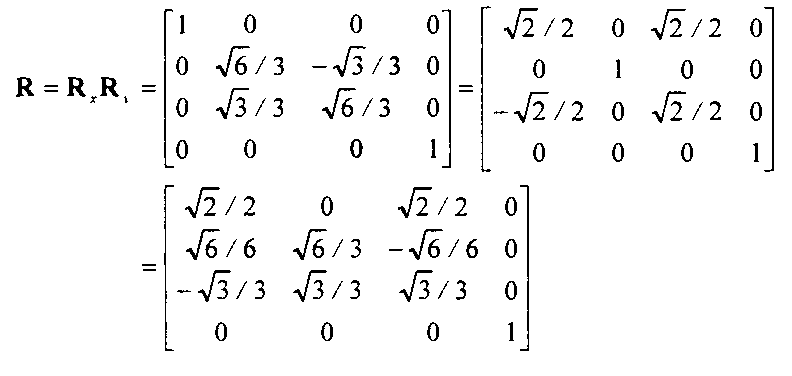
5.2. Размещение камеры
Несложно проверить, что исходная вершина (-1, 1, 1) корректно преобразуется этой матрицей в (О, О, -У! ). Теперь добавим к повороту преобразование сдвига на (0, 0, -а*). Получим:
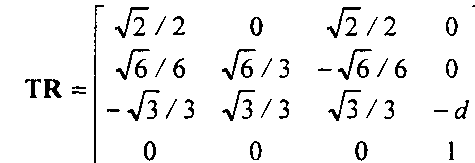
Фрагмент программы, в котором формируется эта матрица вида, имеет следующий вид: д1Ма!г1хМос1е(СЬ_М0ВЕЬУ1Е;?); д1Ьоас!1с1егг1:11у(); glTranslatef(0.0, 0.0, -с!); glRotatef(-35.26, 1.0, 0.0, 0.0); ql9.otd.tQi(45.0, 0.0, 1.0, 0.0); Обратите внимание на то, что функция дЮгт.Ьо() устанавливает параллелепипед видимости относительно фрейма камеры. Таким образом, при ортогональном проецировании сдвиг камеры не влияет на размер изображения, но определяет, попадет ли объект "в кадр" или нет.
5.2.2. Задание ориентации камеры
Я подозреваю, что предыдущий пример с вычислением параметров преобразования вида, необходимых для получения изометрии объекта, вас, мягко говоря, озадачил. Неужели придется вручную вычислять эти параметры, а затем задавать их в программе? Должен вас успокоить - продемонстрированный подход далеко не единственный. Ниже мы рассмотрим другой подход, который реализован в PHIGS и GKS-3D. Как и раньше, начнем с мирового фрейма. Опишем в нем положение и ориентацию камеры. Тип проецирования - параллельное или перспективное - определяется отдельно. Эта процедура эквивалентна спецификации матрицы проецирования в OpenGL. Первую часть процесса визуализации часто называют нормализацией (normalization transformation). Как и раньше, в исходном состоянии камера находится в начале координат мирового фрейма, и ее оптическая ось направлена вдоль отрицательной полуоси z мирового фрейма. Требуется установить камеру таким образом, чтобы она находилась в точке, которую будем называть точкой привязки вида - ТПВ (view-reference point) (рис. 5.15). Положение ТПВ задается в мировом фрейме. Для установки камеры в эту точку в прикладной программе вызывается функция
