Начнем с того, что определим соответствие между положением точки на поверхности шарика трекбола и позицией указателя мыши. Будем рассматривать трекбол, представленный на рис. 4.56, и предположим, что радиус его шарика равен одной единице. Тогда можно поста4.10. Взаимодействие пользователя с трехмерными графическими приложениями 199

вить в соответствие точкам поверхности шарика точки на плоскости у = 0 (рис. 4.57). Точка (.х, у, г) на поверхности шарика проецируется в точку (х, 0, г) на плоскости. Такая проекция обратима, поскольку известно, что трехмерная точка, спроецированная в определенную точку на плоскости, должна удовлетворять соотношению, описывающему сферу:

X +у +2 = 1 .

Следовательно, данной точке (х, 0, г) на плоскости должна соответствовать точка (х, у, 2) на верхней полусфере, где

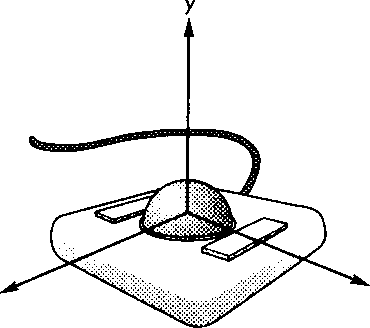
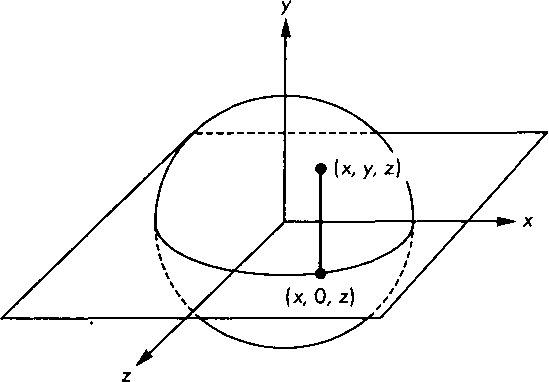
Рис. 4.56. Фрейм трекбола Рис. 4.57. Проекция на плоскость точки на поверхности шарика трекбола Таким образом, по положению указателя мыши на экране можно восстанавливать трехмерную точку на поверхности шарика трекбола. Рассмотрим теперь две точки, р, и р2, на верхней полусфере шарика. Векторы, проведенные из центра шарика к этим точкам, определяют ориентацию плоскости, нормаль к которой можно вычислить как векторное произведение этих векторов (рис. 4.58)"images/tmpB6CA-159.png" alt="Определение плоскости поворота">

Рис. 4.58. Определение плоскости поворота

Объекты и геометрические преобразования

Реализовать обработку положения трекбола можно с помощью функций обработки событий простоя, движения мыши и нажатия кнопок мыши из библиотеки GLUT. Этот процесс можно рассматривать в терминах трех логических переменных или флагов, которые контролируют движение мыши и перерисовку изображения. При инициализации программы этим логическим переменным присваиваются такие значения12"opengl5_217.html">⇐ Предыдущая| |Следующая ⇒