4.8.4. Поворот вокруг произвольной оси

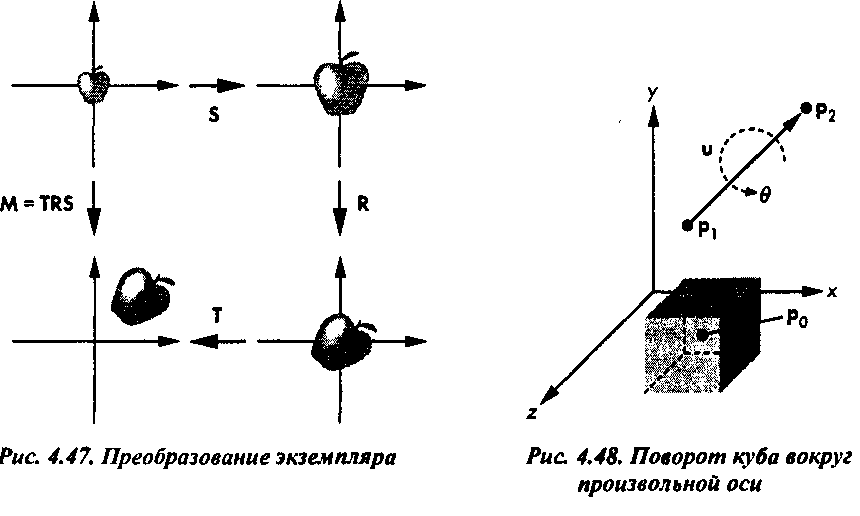
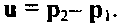
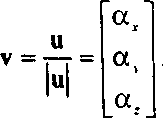
Объекты и геометрические преобразования

Выше уже было показано, что преобразование упрощается, если перенести фиксированную точку в начало координат. Таким образом, первый сдвиг - это Т(-р0), а последний - Т(ро). После начального сдвига задача поворота приобретает вид, как на рис. 4.49.

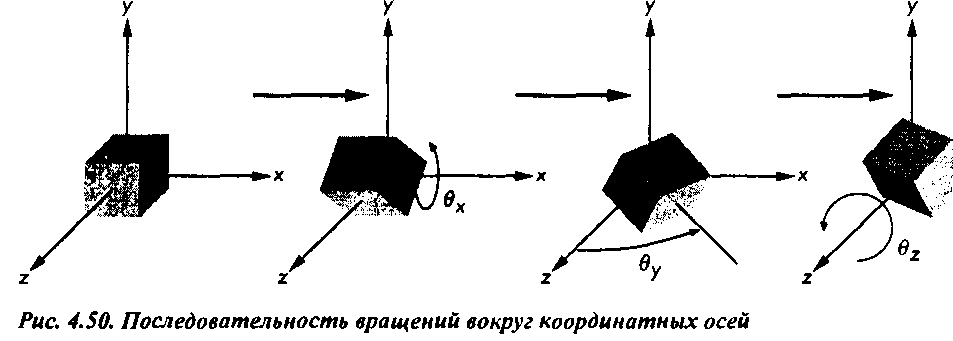
В предыдущем примере (см. раздел 4.8.2) было показано, что поворот вокруг произвольной оси можно свести к последовательности поворотов вокруг отдельных осей координат. Основная загвоздка при этом - определить, на какой угол нужно повернуть вокруг каждой оси. Поэтому применим другую стратегию - выполним два первых поворота таким образом, чтобы ось поворота V совместилась с координатной осью г. Затем повернем вокруг г на заданный угол 8, после чего выполним первые два поворота в обратном порядке и обратном направлении. Таким образом, матрица комплексного преобразования имеет вид произведения: к = кл-е*) я,(-е,) *.-(е*) Л*(0*)Эта последовательность поворотов показана на рис. 4.50. Наиболее сложная часть процедуры - определение вх и 8Г

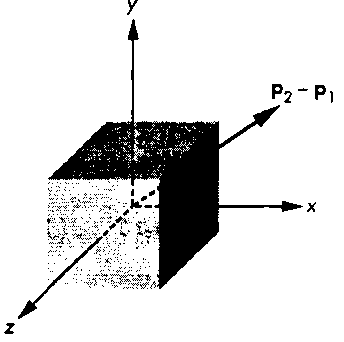
Рис. 4.49. Перенос фиксированной точки в начало координат

Рассмотрим компоненты вектора v. Поскольку v является вектором единичной длины, то а,2 + о^2 + ou2 = 1.

Проведем отрезок от начала координат в точку (о^, Оу, а.). Этот отрезок имеет единичную длину и ориентирован в направлении вектора v. Опустим перпендикуляры из точки (с^, ос,, а.) на каждую координатную ось, как показано на рис. 4.51. Три направляюща угла (direction angles) - фх, фя ф. - это углы между отрезком (или вектором v) и координатными осями. Между направляющими косинусами (direction cosines) и компонентами v существует очевидное соотношение"opengl5_208.html">⇐ Предыдущая| |Следующая ⇒