4.4.2. Внешние и внутренние грани При определении трехмерных многогранников порядок перечисления вершин имеет очень существенное значение. Во фрагменте программы, приведенном выше, мы перечислили вершины первой грани в таком порядке: 0, 3, 2, 1. Перечисление в порядке 1, 0, 3, 2 приведет к тому же результату, поскольку последняя вершина в списке автоматически соединяется с первой. Однако порядок 0, 1, 2, 3 даст совсем иной результат. Хотя таким образом формируется тот же самый контур многоугольника, ребра будут "обходиться" в обратном направлении, как показано на рис. 4.23. Следует учитывать, что многоугольник (точнее, его внутренняя область) имеет две стороны - внешнюю и внутреннюю. Можно отображать любую из них или обе, но в любом случае нужно располагать каким-то методом идентификации сторон.
Объекты и геометрические преобразования
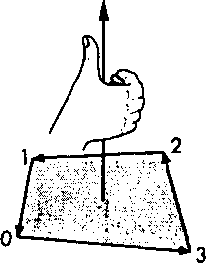
Будем называть грань смотрящей наружу, или внешней (outward facing), если при взгляде с внешней стороны объекта на эту грань ее вершины, расположенные в том порядке, который задан при определении грани, "обходятся" против часовой стрелки. Этот метод определения порядка вершин некоторого контура известен как правило правой руки (right-hand rule), поскольку, если расположить четыре согнутых пальца правой руки вдоль направления обхода контура, большой палец будет указывать наружную сторону грани.
В нашем примере очень важно перечислить при определении первой грани вершины именно в порядке 0, 3, 2, 1, а не 0, 1,2,3, поскольку в Рис 4.23. Обход этом случае внешняя сторона многоугольника будет и внешней по от- вершин много е- б угольника ношению к кубу . J
4.4.3. Структура данных для представления объектов Теперь рассмотрим, каким образом описать с помощью множества вершин объемный объект - куб. Можно, например, вызывать функцию формирования многогранника
glBegin(GL_P0LYG0N)шесть раз, передавая ей каждый раз свой набор из четырех вершин (посредством glVertex()) и завершая список вызовом glEnd(). Можно использовать другой способ - вызвать glBegin(GL QUADS), а затем передать список из 24 вершин, который завершается glEnd(). Оба эти способа будут восприняты графической системой, но при этом, хотя геометрия куба и будет воспроизведена, информация о его топологии как составного объекта будет утеряна. Если рассматривать куб как многогранник, то он представляет собой совокупность шести граней, которые являются многоугольниками с совпадающими вершинами, - каждая вершина принадлежит трем граням. Каждая пара соседних вершин определяет ребро, которое принадлежит двум граням. Приведенные утверждения и описывают топологию шестигранника. Они правомерны независимо от положения конкретных вершин, т.е. от геометрии объекта7.
