Прежде чем перейти к подробному анализу методов выполнения преобразований и реализации этих методов в OpenGL, рассмотрим еще один простой пример. По умолчанию фрейм камеры совмещен с мировым фреймом, причем ось визирования камеры направлена вдоль оси z, но в обратную сторону (рис. 4.21,а). В большинстве приложений объекты сцены, как правило, размещаются вблизи начала координат. Например, квадрат строится относительно своего центра, а группа объектов - вокруг центра масс. Естественно таким же образом настраивать параметры визуализации, чтобы в поле зрения камеры попадали только объекты, расположенные перед ней. Следовательно, для того чтобы сформировать изображение, в котором будут присутствовать все сформированные объекты, нужно либо отодвинуть камеру от объектов, либо отодвинуть объекты от камеры. Это все равно, что сместить фрейм камеры относительно мирового фрейма. Если же рассматривать фрейм камеры как фиксированный, а матрицу вида - как представляющую положение мирового фрейма относительно фрейма камеры, то матрица вида

"10 0 0 "
0 10 0

А =

0 0 1 0 0 0 1

преобразует точку, имеющую в мировом фрейме координаты {х, у, z), в точку, которая во фрейме камеры имеет представление (х, у, z-d). Если задать d достаточно большое положительное значение, то можно "передвинуть" объекты, чтобы они оказались перед камерой (рис. 4.21,6). Учтите, что пользователь - а именно он имеет дело с мировой системой координат - размешает объекты, как и раньше, недалеко от начала координат. Матрица вида определяет только взаимное положение фреймов. Использовать такой подход гораздо удобнее и логичнее, чем изменять параметры вершин объектов, чтобы разместить их перед камерой.

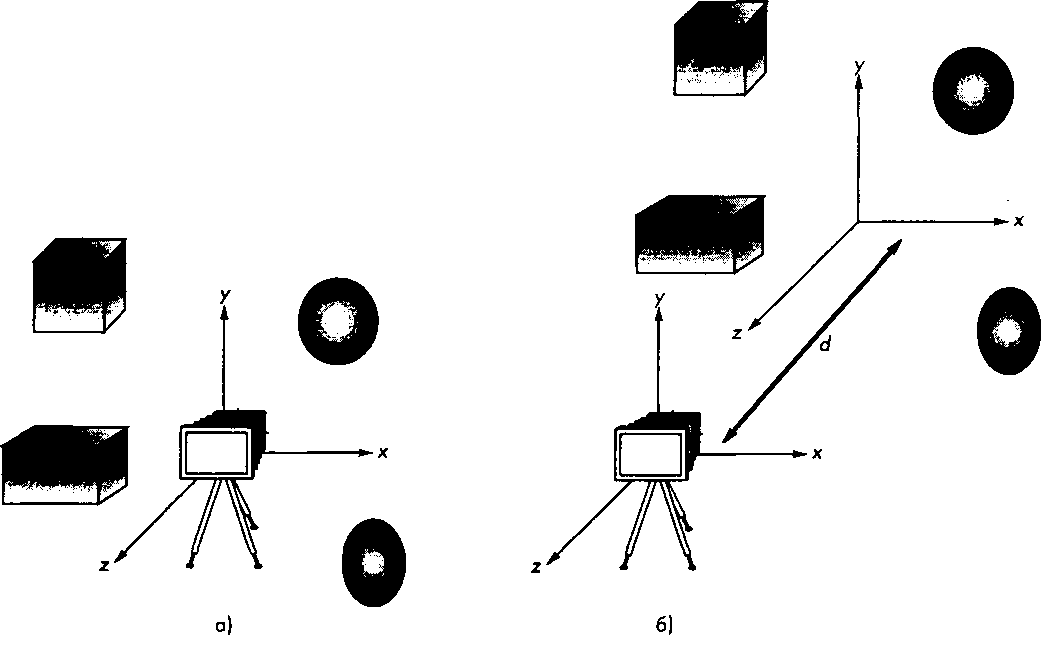
Рис 4.21. Фреймы камеры и мировой: а - исходное положение по умолчанию; б-размещение после задания матрицы вида

168 Глава 4. Объекты и геометрические преобразования В OpenGL матрицу вида можно задать поэлементно, передав 16 чисел в качестве аргументов функции glLoadMatrix( ). Однако не ясно, как определить нужные значения элементов. При решении геометрических задач мы всегда мыслим категориями последовательных преобразований (элементарных переходов), таких как плоскопараллельные смешения, повороты и изменения масштаба. Этому подходу мы и последуем в дальнейшем.

⇐ Предыдущая| |Следующая ⇒