у* = у cos (а) - zsin(cc) = 0 0 - 1 1 = -1; z1 = у cos (а) + z cos (а) = 0 1 + 1 0 - 0.
В результате этих преобразований вектор примет направление, противоположное оси У. Можно проверить самостоятельно, что поворот на 90° вектора (0,1, 0), направленного вдоль оси У, совместит его с осью Z.
Таким образом, на плоскости YZповорот орта первой оси Уна 90° всегда совмещает его со второй осью Z, но на рис. 24.2 видно, что, если смотреть на плоскость YZ из положительной полуоси Ху поворот орта происходит в одной системе координат против часовой стрелки, а в другой системе - по часовой стрелке. Для вращения объектов при помощи графических библиотек программист может заполнить элементы матрицы самостоятельно или применять библиотечные функции, которым для формирования матрицы вращения надо задать угол поворота и ось, вокруг которой выполняется поворот. Чтобы при применении стандартных функций получить именно желаемый визуальный эффект, надо учитывать, для какой системы координат формируется функция, а также другие факторы. Нужно знать, как реализовано в библиотеке перемножение матрицы и вектора, что именно вращается - объект или система координат, и даже знать, как хранится матрица в памяти.
При выполнении преобразований умножением матрицы на столбец приведенные выше матрицы вращения надо транспонировать. При этом поворот в плоскости XYзапишется следующим образом:
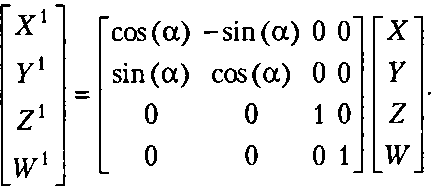
Как и в двумерном случае, преобразование может интерпретироваться не как поворот точки вокруг оси, а как вычисление координат неподвижной точки в новой системе координат, повернутой относительно старой на заданный угол. Если значение а определяет угол поворота координатных осей, то матрицы надо также транспонировать.
Предположим, что положение летательного аппарата характеризуют его координаты:
float XNab.YNab.ZNab:Геометрические преобразования
Направления взгляда пилота задаются при помощи трех углов: float Alpha. AlphaX. AlphaZ; Переменная Alpha задает угол поворота наблюдателя вокруг мировой оси У, тангаж Al phaX указывает угол поворота вокруг направления оси X, полученного поворотом на угол Al pha. Крен Al phaZ задает угол поворота вокруг того положения оси Z наблюдателя, которое получено двумя предыдущими вращениями.
