Теперь следует рассмотреть применение матриц для выполнения элементарных геометрических преобразований в однородных координатах.
Перенос и масштабирование модели объекта Получить результат (х\ y\zx) сдвига вершины (х, г/, z) на Сх единиц по оси X и Су, С2 единиц вдоль осей У и Z можно после перехода к однородным координатам при помощи выражения
. FLOAT _14.
. FLOAT _24.
. FLOAT _34.
. FLOAT 44);Геометрические преобразования
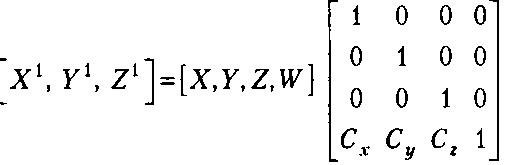
(24.3).Если обозначить в (24.3) векторы вершин как Vі, V, а матрицу сдвига через С, то данное выражение можно записать в виде Vі = УС.
Действительно, производя умножение строки на матрицу, можно получить: Х{ = Х + \¥СХ,У{ =\ + ШХ,1^ =1 + Шх,Ух Теперь возвратимся к декартовым координатам на плоскости:
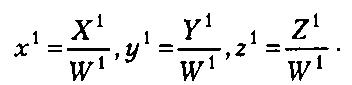
В правых частях полученных выражений нужно выразить 1У1 через IV, а Xх через X:
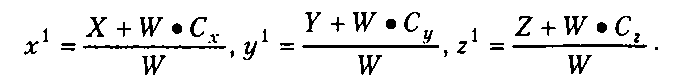
После замены однородных координат декартовыми (X = У - №У, 2 = 1У7) и сокращения правых частей на 1^ можно получить результат вычисления выражения (24.3) не в матричной форме: Можно рассматривать эти выражения как перенос вершины на (Сх, Су1 С2) в неподвижной системе координат или как вычисление координат неподвижной вершины в новой системе, начало которой сдвинуто относительно исходной на (-Сх,
-су,-сг).
Аналогичные рассуждения показывают, что для масштабирования объекта нужно все его вершины преобразовать в соответствии со следующим выражением:
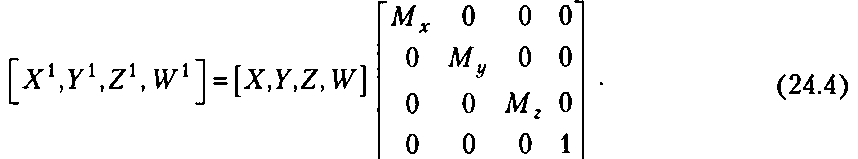
Обозначив матрицу масштабирования через М, можно записать данное выражение как Vх = УМ.
Рассмотренные выражения позволяют выполнить последовательность операций масштабирования и сдвига одним умножением вектора на матрицу. Для начала следует применить к вершине У операцию масштабирования Vх = УМ. К полученной вершине нужно применить операцию сдвига V1 = УС. В правой части последнего равенства нужно выразить значение Vх через У - У1 - УМС.
Преобразования в пространстве Эти преобразования показывают, что матрица объединенного преобразования равна произведению матриц МС, причем матрицы в произведении записываются слева направо в том порядке, в каком выполнялись преобразования.
