Стандартный подход заключается в использовании 32-битовых целых чисел (long), где младшие 16 бит отводятся под дробную часть числа, а старшие 16 бит -под целую. Таким образом, каждому вещественному числу/ставится в соответствие целое число / == [2У6/]. Подобное представление обозначается как 16.16, показывая сколько бит отводится под целую и дробную части. Возникающая погрешность не превышает 216. Рассмотрим, каким образом осуществляются операции над такими числами.
Очевидно, что сумме (разности) чисел/1 и /2 соответствует сумма (разность) чисел I] и /2, так как
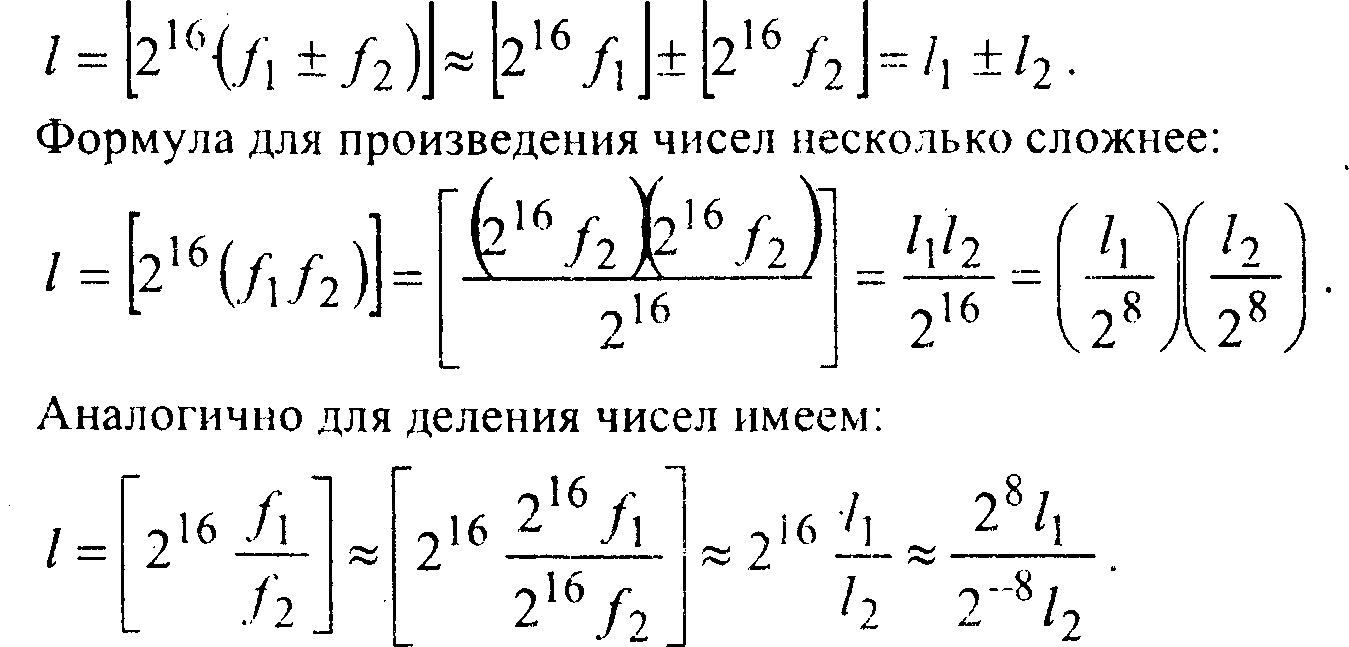
Умножение и деление на степени двойки легко заменяются побитовыми сдвигами.
Таким образом, сложению, вычитанию и сравнению чисел с фиксированной точкой соответствуют сложение, вычитание и сравнение соответствующих 32-битовых чисел. Умножению и делению соответствуют умножение и деление с дополнительными сдвигами.
При умножении следует обратить внимание на то, что при перемножении достаточно больших чисел результат может легко выйти за отведенные 32 бита. Для компенсации этого производятся предварительные сдвиг и, а не только .тишь сдвиги результата операции.
іШОҐ/ПИСОИ
Компьютерная графика. Полигональные модели Естественным шагом для повышения быстродействия является также отказ от вычисления "на ходу" значений тригонометрических и других сложных функций. Вместо этого удобнее использовать таблицы, где хранятся значения требуемых функций (с некоторым шагом).
Ниже приводятся тексты простейшей библиотеки, реализующей работу с тригонометрическими функциями в описанном представлении.
SI // File Fixmath.h
#ifndef __FIXED_MATH___
#define _FIXED_MATH__
#define ANGLE_90 16384U // angle of 90 degrees
#define ANGLEJ80 32768U // angle of 180 degress
#define ANGLE_270 49152U // angle of 270 degress
#define MAX_FIXED 0x7FFFFFFFI // maximum possible Fixed number
#define ONE 0x100001 // 1.0
typedef long Fixed; typedef unsigned short Angle;
extern Fixed * sinTable;
extern Fixed * cosTable;