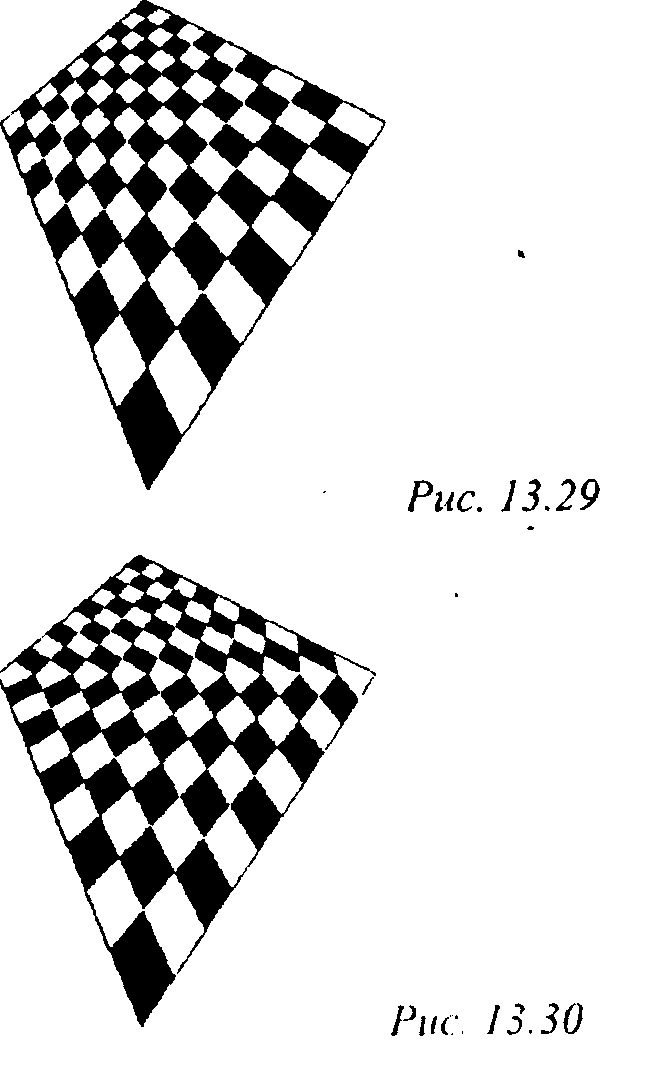
Более точным является подход, при котором грань рисуется по строкам (столбцам) с применением линейной интерполяции внутри каждой строки, но значения параметров для каждой строки вычисляются точно.
Получающееся при этом изображение приведено на рис. 13.30.
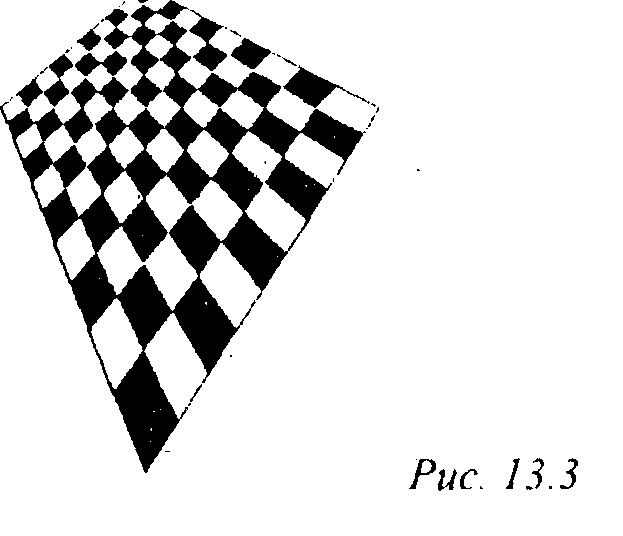
Более высокой точности можно добиться, применяя квадратичную интерполяцию. Получающееся при этом изображение приведено на рис. 13.31.
Можно использовать и кубическую интерполяцию: и = а0 + а IX + а2х2 + а^х\
где вместо задания значений в промежуточных точках обычно задаются значения производных в конечных точках
Компьютерная графика. Полигональные модели И,(Х|) = М,|,' //(х2) =1/2, м'(х2) = и* гДля вычисления значений производных можно воспользоваться следующими соотношениями:
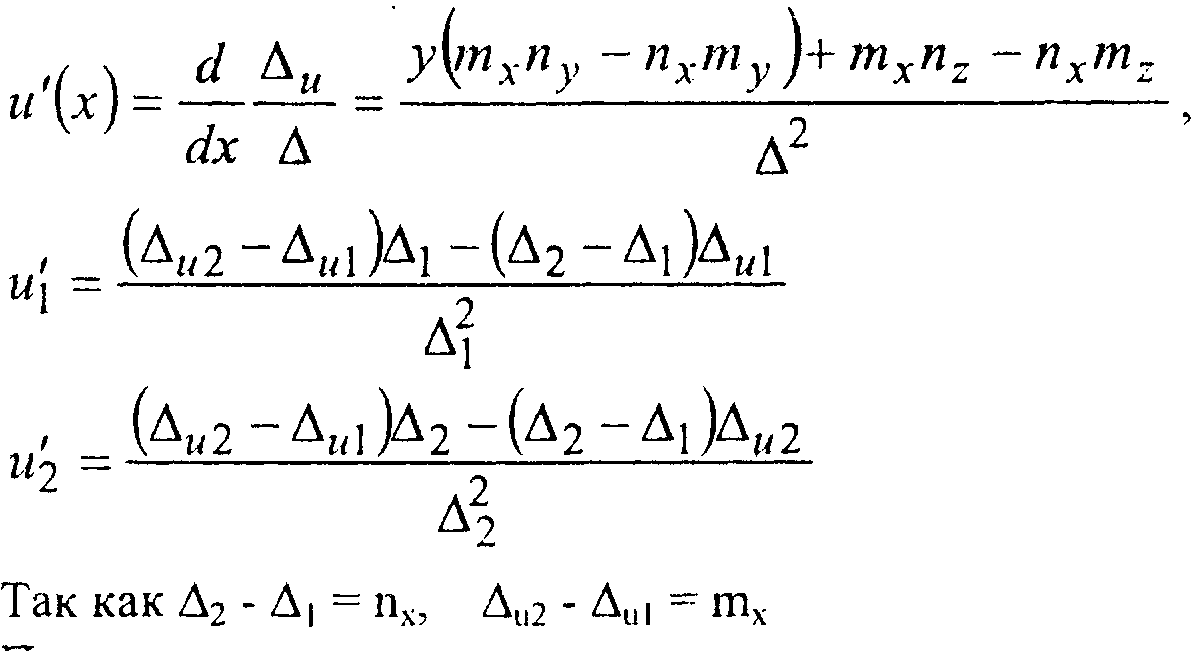
полагая, как и ранее, что аргумент* изменяется на отрезке [и, lJ, получаем дующие формулы для интерполяционных коэффициентов: а0 = ии ал = и',, а2 = 3(и2 - и\) - 2w'i - и'2, а3 = -2{и2 - и\) + и\ + и\.
Для расчета текстуры вдоль строки пикселов можно воспользоваться еле щим фрагментом программы: и void cubic () {
float dx01 = (float)(prf1].x - pr[0].x)/(float)(pr[1].y - pr[0].y);
float dx12 = (fioat)(pr[2].x - pr[1].x)/(float)(pr[2].y- pr[1].y);
float dx03 = (float)(pr[3].x - pr[0].x)/(float)(pr[3].y - pr[0].y);
float dx32 = (float)(pr[2].x - pr[3].x)/(float)(pr[2].y - pr[3].y);
float x1 = pr [0].x;
float x2 = pr [0].x;for (int у = pr [0].y; у < pr [2].y; y++ ) {
float du1 = t.x [0][0] * x1 + t.x [0][1] * у + t.x [0][2];
float dv1 = t.x [1][0] * x1 + t.x [1][1] * у + t.x [1][2];
float d1 = t.x [2][0] * x1 + t.x [2][1] * у + t.x [2][2];
float du2 = t.x [0][0] * x2 + t.x [0][1] * у + t.x [0][2];
float dv2 = t.x [1][0] * x2 + t.x [1][1] * у + t.x [1][2];
float d2 = t.x [2][0] * x2 + t.x [2][1] * у + t.x [2][2];
float invDx = x2 > x1 ? 1.0 / ( x2 - x1 ): 0.0;
float tt1 = ( du2 * d1 - du1 * d2 ) * invDx;
float «2 = ( dv2 * d1 - dv1 * d2 ) * invDx;13. Элементы виртуальной реальн
float tt3 = «1 / ( 62 * 62 );