Подобный подход позволил получить крайне динамические трехмерные сцены, состоящие из полигональных объектов.
Дтя рендеринга каждый объект как точка сравнивается со всеми разбивающими плоскостями и в нужном месте выводится как независимое BSP-дерево.
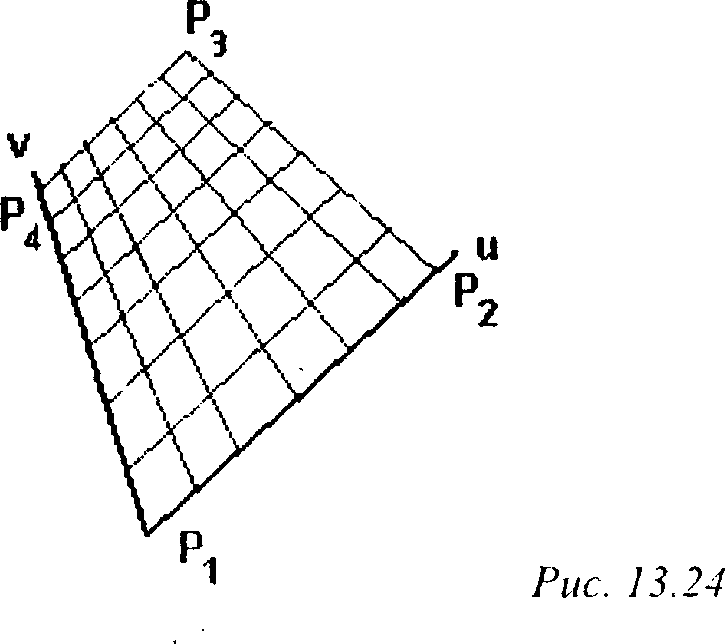
13.5. Текстурирование в общем случае Рассмотрим, каким образом можно осуществить текстурирование произвольно ориентированной грани при перспективном проектировании (рис. 13.24).
Пусть грань Р задана в пространстве набором своих вершин Рь Р2, Рз, Р^ Будем считать ее прямоугольной и определим вектор а как Рь а также два боковых вектора в) и е2.
е, = Р2-Р, е2=Р4-Р,
13. Элементы виртуальной реальности Нормаль п к грани определяется из соотношения п = [е}, е2].
Будем считать, что перспективное преобразование осуществляется по формулам
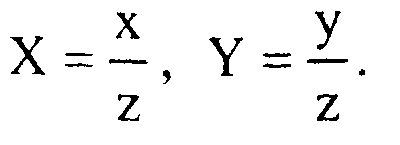
т. е. в данном случае г соответствует глубине.
Найдем образ произвольной точки грани р = а + ие\ + уе2, где и и v - параметры текстуры. После несложных преобразований получаем:
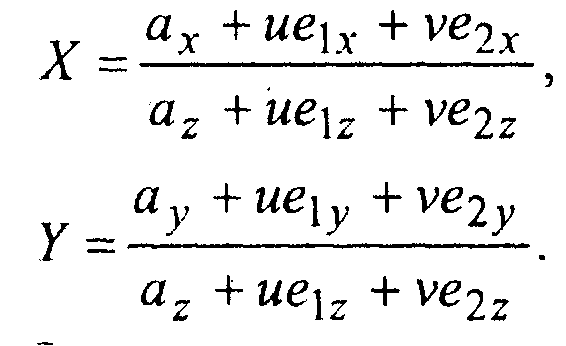
Однако для текстурирования грани удобнее использовать обратное отображение. Найдем прообраз (и, у) произвольной точки (X, У) экрана. Для этого разрешим предыдущие соотношения относительно и и v. Умножив их на знаменатель дроби, получим систему линейных уравнений относительно и и у;
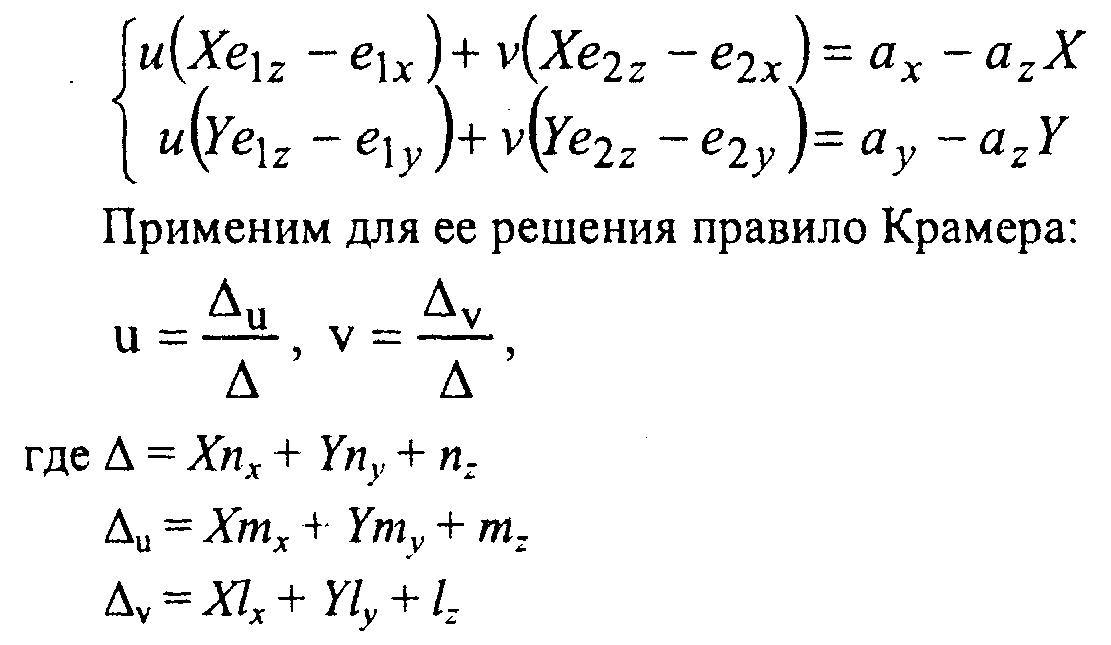
Вспомогательные векторы / и/и определяются следующими векторными произведениями: т = [е2, а], /= [а, Эти формулы можно переписать с использованием однородных координат в виде В общем случае перспективное проектирование задается формулой
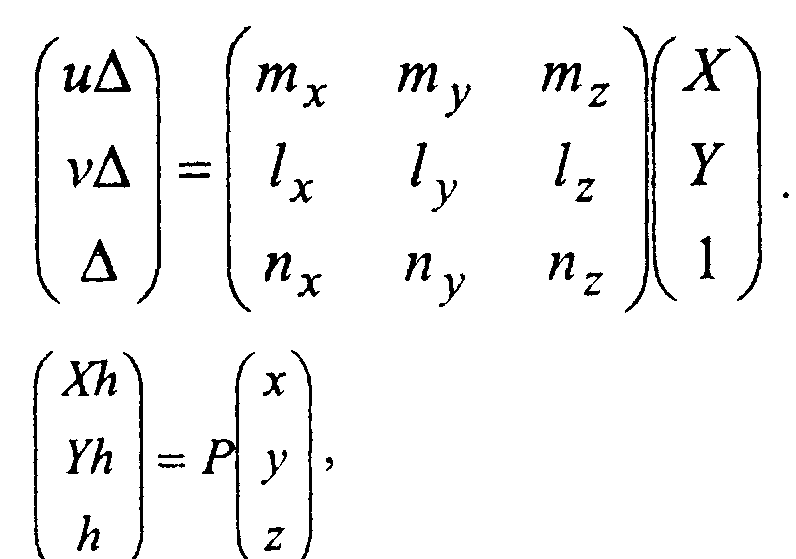
где Р - невырожденная матрица; например следующему преобразованию: Компьютерная графика. Полигональные модели
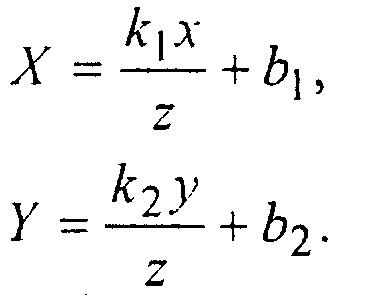
соответствует матрица
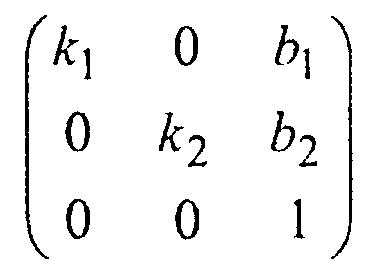
Для определения параметров текстуры можно воспользоваться такой формулой:
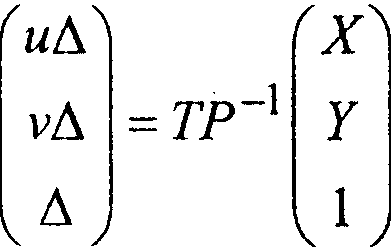
где T - матрица, составленная из векторов m, / ил.
Величины w и v определяют точку текстуры в единичном квадрате, т. е. вершине Р\ соответствует и - 0, v = 0, вершине Р2-и- 1, v = 0, вершине - и - 1, v = 1 и вершине Р¥ - и = 0, v = 1. Чтобы получить индексы для текстуры, например размера 64 на 64, следует взять [64*и] и [64*v],
