int y1 = getmaxy () - 40;
line (xO, y0, x1, yO ); line ( x1, yO, x1, y1 ); line (x1, y1, xO, y1 ); line (xO, y1, xO, yO );
float kx = ( x1 - xO ) / ( xMax - xMin ); float ky = ( y1 - yO ) / ( yMax - yMin ); float x = a; float h =(b-a)/100.0;
moveto ( xO + (x - xMin) * kx, yO + (yMax - fVal [0]) * ky );
for (i = 1; i < 100; i++, x +=»h )
lineto ( xO + (x-xMin)*kx, yO + (yMax-fVal [i])*ky);
char str [128];
settextstyle ( SMALL^FONT, HORI2_DIR, 1 );
for ( x = xMin; x <= xMax; x += xStep ) {
int ix = xO + (x - xMin ) * kx;
line (ix, y1, ix, y1 + 10 );
if ( x + xStep <= xMax )
for (i = 1; i < 10; i++ )
line (ix + i*xStep*kx*0.1, y1, ix + i*xStep*kx*0.1, y1 + 5 );
sprintf ( str, "%g", x );
outtextxy (ix - textwidth (str) / 2, y1 + 15, str);
}
for (float y = yMin; y <= yMax; y += yStep ) {Компьютерная графика. Полигональные модели
int iy = yO + ( yMax - у ) * ky;
line ( xO -10, iy, xO, iy );if ( у + yStep <= yMax )
for (i = 1; i < 10; i++ )
line ( xO - 5, iy - i*yStep*ky*0.1,
xO, iy-i*yStep*ky*0.1 );sprintf ( str, "%g", у );
outtextxy ( xO -10 - textwidth ( str), iy, str);
}
delete fVal;
}Построение графика функции двух переменных будет подробно рассмотрено в гл. 10.
Здесь мы приведем лишь процедуру построения изолиний функции двух переменных, т. е. семейства линий, на которых эта функция сохраняет постоянные значения.
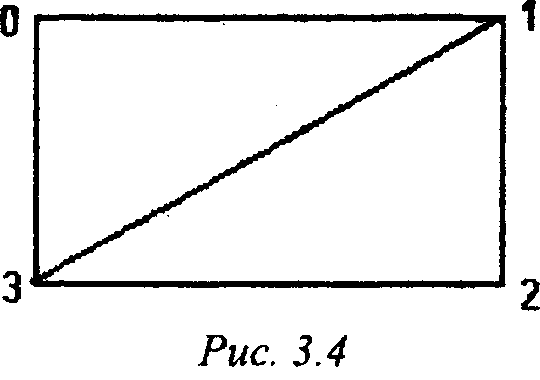
Для* этого вся область изменения аргументов разбивается на набор прямоугольников, каждый из которых затем делится диагональю на два треугольника (рис. 3.4).
В каждом треугольнике заданная функция приближается линейной функцией, график которой проходит через соответствующие вершины, при этом участок изолинии, лежащий в данном треугольнике, является отрезком прямой, соединяющим точки пересечения сторон треугольника с плоскостью z = const. Приведенная ниже процедура для такого треугольника строит все содержащиеся в нем изолинии.
53 // File example7.cpp struct Point
{
int x; int y;
};
void plotlsolines (float xO, float yO, float x1,