Доказательство этого утверждения можно найти в [15].
Среди всех возможных триангуляции выделяется специальный вид - так называемая триангуляция Делоне. Эта триангуляция является хорошо сбалансированной в том смысле, что формируемые ей треугольники стремятся к равноугольности.
Определение. Триангуляция набора точек S называется триангуляцией Делоне, если окружность, описанная вокруг каждого из треугольников, не будет содержать внутри себя точек набора S.
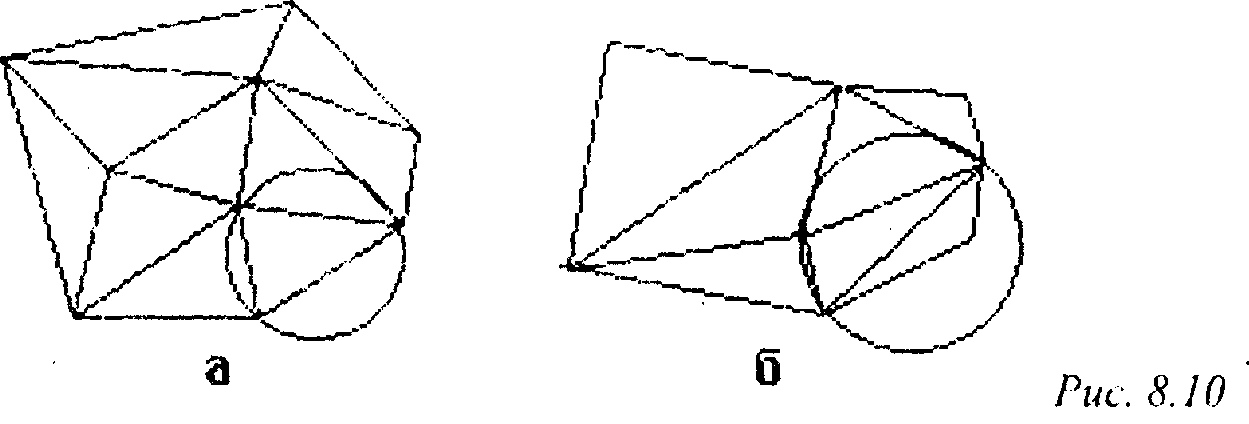
На рис. 8.10, а показана окружность, не содержащая внутри себя точек набора S. Триангуляция, приведенная на рис. 10, б, не является триангуляцией Делоне, так как существует окружность, содержащая внутри себя одну из точек набора.
Компьютерная графика Полигональные модели
Для .упрощения алгоритма триангуляции сделаем два предположения относительно набора S: 1) чтобы триангуляция вообще существовала, необходимо, чтобы набор S содержал по крайней мере 3 неколлинеарные точки; 2) никакие 4 точки из набора S не лежат на одной окружности. Если последнее предположение не выполнено, то можно построить несколько различных триангуляции Делоне (см. упражнение 6).
Предлагаемый ниже алгоритм работает путем постоянного наращивания текущей триангуляции (по одному треугольнику за шаг). На каждой итерации алгоритм ищет новый треугольник, который подключается к текущей триангуляции.
В процессе триангуляции все имеющиеся ребра делятся на три класса:
спящие ребра - ребра, которые еще не были обработаны алгоритмом;
живые ребра - ребра, для каждого из которых известна только одна примыкающая к нему область;
мертвые ребра - ребра, для каждого из которых известны обе примыкающие к нему области.
Вначале живым является единственное ребро, принадлежащее границе выпуклой оболочки, а все остальные ребра - спящие. По мере работы алгоритма ребра из спящих становятся живыми, а затем мертвыми.
На каждой итерации алгоритма выбирается одно из ребер границы и для него находится область, которой это ребро принадлежит. Если найденная область является треугольником, определяемым концевыми точками ребра и некоторой третьей точкой, то это ребро становится мертвым, поскольку известны обе примыкающие к нему области. Каждое из двух других ребер этого треугольника переводится или из спящего в живое или из живого в мертвое
