swap ( s [a], s [i]);
p -> addVertex ( s [I], p -> numVertices ); a = i + 1;
for (int j = i + 2; j <= n; j++ ) {int с = s [j].classify ( s [i], s [a]);
if ( с == LEFT || с == BEYOND) a = i;
}
if ( a == n ) return p;
}
return NULL;Компьютерная графика. Полигональные модели Временные затраты данного алгоритма равны 0(1т), где Л - число вершин в границе искомой выпуклой оболочки. Работа данного алгоритма проиллюстрирована на рис. 8.7
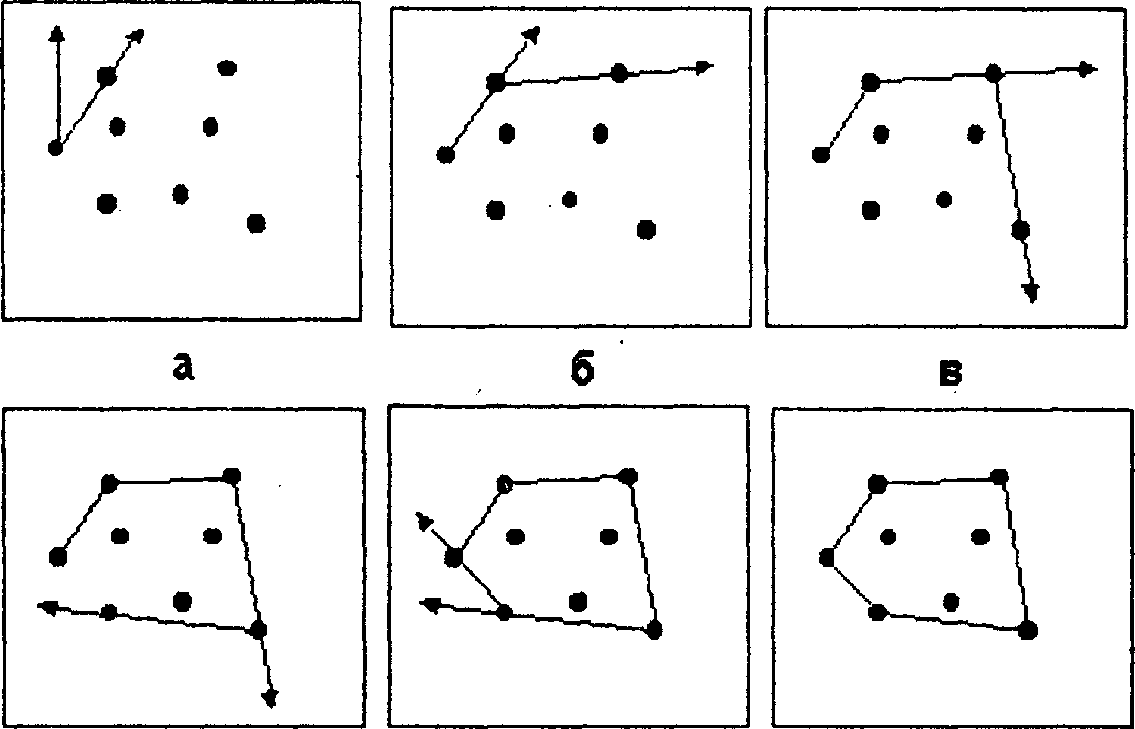
Рис. 8.7
Рассмотрим еще один алгоритм для построения выпуклой оболочки, так называемый метод обхода Грэхема. В этом методе выпуклая оболочка конечного набора точек S находится в два этапа. На первом этапе алгоритм выбирает некоторую экстремальную точку а е S и сортирует все остальные точки в соответствии с углом направленного к ним из точки а луча. На втором этапе алгоритм выполняет пошаговую обработку отсортированных точек, формируя последовательность многоугольников, которые в конце концов и образуют искомую выпуклую оболочку convS.
Выберем в качестве экстремальной точки точку с минимальной у-координатой и поменяем ее местами с s0. Остальные точки сортируются затем в порядке возрастания полярного угла относительно точки sq. Если две точки имеют одинаковый полярный угол, то точка, расположенная ближе к % должна стоять в отсортированном списке раньше, чем более дальняя точка. Это сравнение реализуется рассмотренной ранее функцией polarCmp.
Для определения того, какая именно точка должна быть включена в границу выпуклой оболочки после точки Sj, используется тот факт, что при обходе границы выпуклой оболочки в направлении по часовой стрелки каждая ее вершина должна соответствовать повороту влево.
// File graham.срр #include <stdlib.h> #include "polygon.h" #include "stack.h"
template <class T> void swap ( T a, T b )о
JJL
{
Tc;с = a; a = b; b = a;
8. Основные алгоритмы вычислительной геометрии
Polygon * grahamScan ( Vector2D s [], int n ) {
// step 1 for (int i = 1, m = 0; i < n; i++ ) if(s[i]<s[m]) m = i;
swap ( s [m], s [0]);