- умножение матрицы на вектор
- деление на число;
- поэлементное деление векторов;
- скалярное произведение векторов;
- компонента вектора.
Стандартные приоритеты операций сохраняются.
Кроме этих операций определяются также некоторые простейшие функции для работы с векторами: length () - длина вектора, polar Angle () - полярный угол для вектора, classify () - классификация вектора относительно двух других векторов (точек) (о последней функции подробнее в гл. 8).
С использованием этих классов можно в естественной и удобной форме записывать сложные векторные и матричные выражения.
7.2. Однородные координаты точки Для решения рассматриваемых далее задач весьма желательно охватить матричным подходом все 4 простейших преобразования (в том числе и перенос), а, значит, и общее аффинное преобразование. Этого можно достичь, например, так: перейти к описанию произвольной точки плоскости не упорядоченной парой чисел, как это было сделано выше, а упорядоченной тройкой чисел.
Пусть М - произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы.
Однородными координатами этой точки называется любая тройка одновременно неравных нулю чисел х\, Л'2, х3, связанных с заданными числами х и у следующими соотношениями: х
У
ХХз ~3 При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М(х, у) плоскости ставится в соответствие точка М{х, у, 1) в пространстве (рис. 7.8).
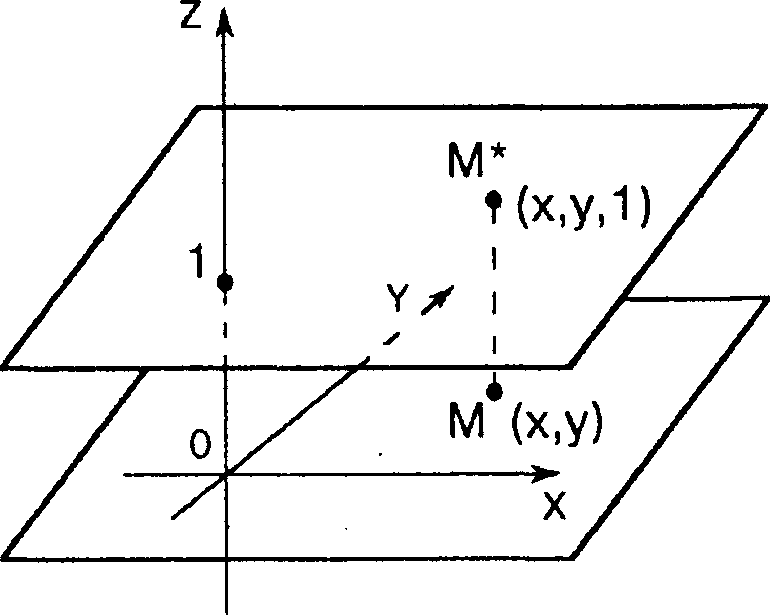
Рис. 7.8
7. Преобразования на плоскости Заметим, что произвольная точка на прямой, соединяющей начало координат, точку 0(0,0,0), с точкой М(х, у, У), может быть задана тройкой чисел вида (Их, Ну, Н). Будем считать, что Н * 0.
Вектор с координатами (Их, Ну, Н) является направляющим вектором прямой, соединяющей точки О(0, 0,0) и М(х, у, 1). Эта прямая пересекает плоскость 2 - 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху.
Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (Их, Ну, И), Н * 0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа Их, Ну, Н новыми координатами этой точки.
