у = хътср + у соб ср.
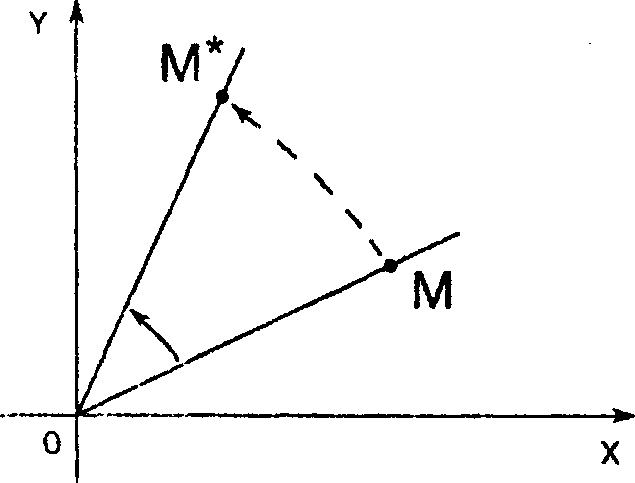
Рис. 7.4
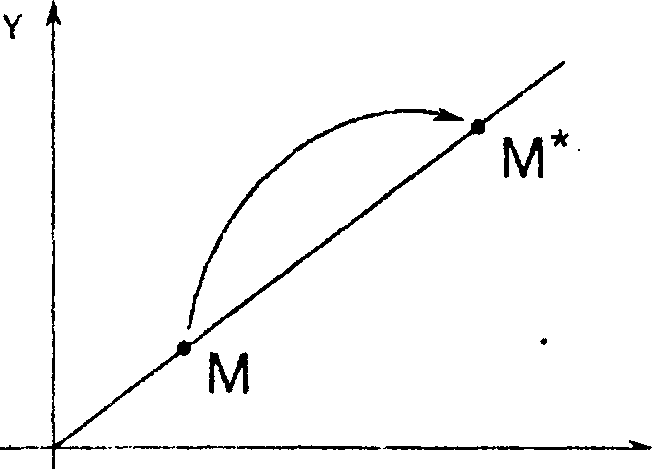
Б. Растяжение (сжатие) вдоль координатных осей можно задать так:
X = (XX,у* = 8у, <х> 0 , д> 0 .
Растяжение (сжатие) вдоль оси абсцисс обеспечивается при условии, что а > 1 (а < 1). На рис. 7.5 а=3>\.
и Рис. 7.5
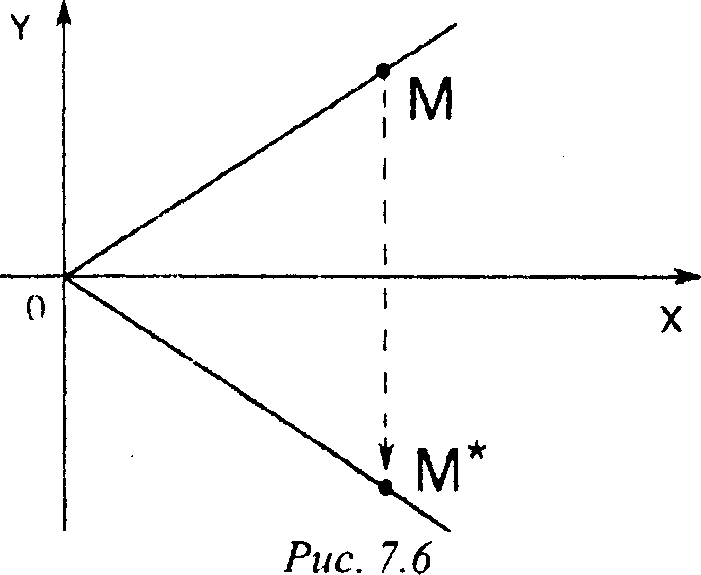
7. Преобразования на плоскости В. Отражение (относительно оси абсцисс) (рис. 7.6) задается при помощи формул х =х,
*у
1-Г. На рис. 7.7 вектор переноса ММ имеет координаты Я, и р. Перенос обеспечивают соотношения х* = х + Я, о
/ М
М
Л*с. 7.7
Выбор этих четырех частных случаев определяется двумя обстоятельствами.
каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы);
как доказывается в курсе аналитической геометрии, любое преобразование вида (7.1) всегда можно представить как последовательное исполнение (суперпозицию) простейших преобразований вида А, Б, В и Г (или части этих преобразований).
Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (7.1) можно описать при помощи отображений, задаваемых формулами А, Б, В и Г.
Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям А, Б и В, строятся легко и имеют соответственно следующий вид:
0Л(\ <Л
r cos<p ъ\г\<р\ (
V
a 0
V
JНиже приводятся файлы, реализующие классы Vector2D и Matrix2D для работы с двух мерной графикой.
0 // File vector2d.h
#ifndef ___VECTOR2D__ #define _VECTOR2D_
#include <math.h>Компьютерная графика. Полигональные модели
enum // values of Vector2D :: classify
{
LEFT, RIGHT, BEHIND, BEYOND, ORIGIN, DESTINATION, BETWE
};
class Vector2D {
public:
float x, y;
Vector2D () {}
Vector2D (float px, float py ) . {
x = px;
y = py;
}
Vector2D ( const Vector2D& v ) {
x = v.x; y = v.y;
}
Vector2D& operator = ( const Vector2D& v ) {
x = v.x; y = v.y;
return *this;
}
Vector2D operator + () const {