6.5. Заполнение многоугольника Рассмотрим, каким образом можно заполнить многоугольник, задаваемый замк нутой ломаной линией без самопересечений.
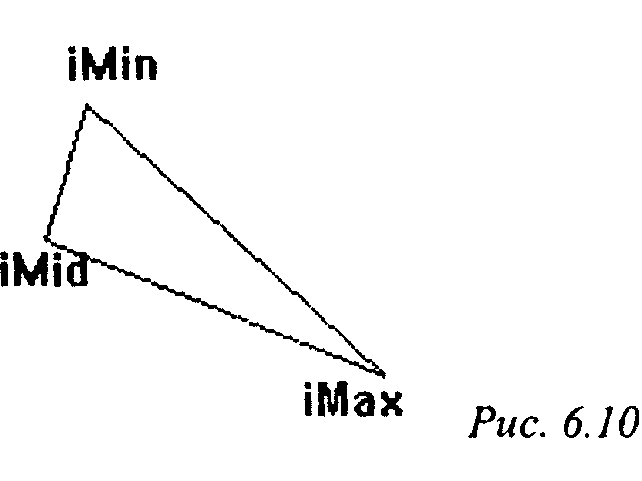
Приведенная ниже процедура осуществляет заполнение треугольника, заданного массивом своих вершин (рис. 6.10). Для отслеживания изменения х-координат вдоль ребер используются числа с фиксированной точкой в формате 16.16 (подробнее об этом - в приложении).
0 // File filltr.cpp
#include <graphics.h> #include "FixMath.h"
struct Point
{
int x; int y;
};
void fillTriangle ( Point p Q ) {
int iMax - 0; int iMin = 0; int iMid = 0;
for (int i = 1; i < 3; i++ ) // find indices of top if ( P Wy < P [iMin].y ) // and bottom vertices iMin = i;
elseКомпьютерная графика. Полигональные модели
if ( р р].у > р [iMaxJ.y ) іМах = і;
iMid = 3 - iMin - іМах; // find index of
// middle item
Fixed dx01 = p [iMaxJ.y 1= p [iMinJ.y ?int2Fixed ( p [iMaxJ.x - p [iMinJ.x ) / ( p [іМах].у - p [iMin].y): Ol;
Fixed dx02 = p [iMin].y != p [iMid].y ?
lnt2Fixed ( p pMidJ.x - p pMinJ.x ) / ( p [iMid].y - p [iMinJ.y ): 01;
Fixed dx21 = p [iMid].y l= p [iMax].y ?
lnt2Fixed ( p [iMax].x - p [iMidJ.x ) / ( p [iMaxJ.y - p [iMid].y ): Ol;
Fixed x1 = int2Fixed ( p [iMin].x ); Fixed x2 = x1;
for (і = p [iMinJ.y; і <= p [iMid].y; i++ ) {
line (fixed2lnt ( x1 ), i, fixed2lnt ( x2 ), і); x1 +=dx01; x2 += dx02;
}for (і = p [iMid],у + 1; і <= p [iMaxJ.y; i++ ) {
x1 += dx01; x2+=dx21;
line (fixed2lnt ( x1 ), i, fixed2lnt ( x2 ), і);
}
}Прежде чем перейти к общему случаю, рассмотрим, как осуществляется заполнение выпуклого многоугольника. Заметим, что невырожденный выпуклый многоугольник может содержат не более двух горизонтальных отрезков - вверху и внизу.
Для заполнения выпуклого многоугольника найдем самую верхнюю точку и определим два ребра, выходящие из нее. Если одно из них (или оба) являются горизонтальными, то перейдем в соответствующем направлении к следующему ребру, и так до тех пор, пока у нас не получатся два ребра, идущие вниз (при этом они могут выходить из разных точек, но эти точки будут иметь одинаковую ординату).
